题目内容
已知正方形ABCD的边长为1,分别取边BC、CD的中点E、F,连结AE、EF、AF,以AE、EF、FA为折痕,折叠使点B、C、D重合于一点P.(1)求证:AP⊥EF;
(2)求证:平面APE⊥平面APF;
(3)求异面直线PA和EF的距离.
(1)证明:如下图,∵∠APE=∠APF=90°,PE∩PF=P,∴PA⊥平面PEF.
∵EF平面PEF,∴PA⊥EF.
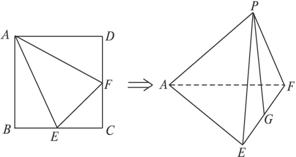
(2)证明:∵∠APE=∠EPF=90°,AP∩PF=P,∴PE⊥平面APF.又![]() PE平面PAE,∴平面APE⊥平面APF.
PE平面PAE,∴平面APE⊥平面APF.
(3)解:在面PEF中,作PG⊥EF,垂足为G,
∵AP与面PEF垂直,PG![]() 平面PEF,
平面PEF,
∴AP⊥PG,PG⊥EF,PG是AP与EF的公垂线.在等腰Rt△PEF中,PE=PF=![]() ,∠EPF=90°,∴PG=EG=
,∠EPF=90°,∴PG=EG=![]() .
.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
已知正方形ABCD的边长为1,设
=
,
=
,
=
,则|
-
+
|等于( )
| AB |
| a |
| BC |
| b |
| AC |
| c |
| a |
| b |
| c |
| A、0 | ||
B、
| ||
| C、2 | ||
D、2
|
 已知正方形ABCD的边长为2,中心为O,四边形PACE是直角梯形,设PA⊥平面ABCD,且PA=2,CE=1,
已知正方形ABCD的边长为2,中心为O,四边形PACE是直角梯形,设PA⊥平面ABCD,且PA=2,CE=1, 如图,已知正方形ABCD的中心为E(-1,0),一边AB所在的直线方程为x+3y-5=0,求其它三边所在的直线方程.
如图,已知正方形ABCD的中心为E(-1,0),一边AB所在的直线方程为x+3y-5=0,求其它三边所在的直线方程.