题目内容
【题目】在四棱锥![]() 中,
中,![]() 为梯形,
为梯形,![]()
![]()
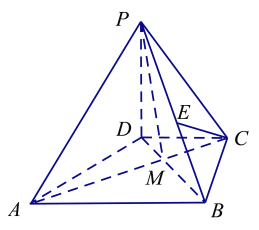
(1)点![]() 在线段
在线段![]() 上,满足
上,满足![]() 平面
平面![]() ,
,![]() ,求
,求![]() 的值
的值
(2)已知![]() 与
与![]() 的交点为
的交点为![]() ,若
,若![]() ,且平面
,且平面![]() 平面
平面![]() ,求二面角
,求二面角![]() 平面角的正切值
平面角的正切值
【答案】(1)![]() ,(2)
,(2)![]()
【解析】
(1)首先延长![]() ,
,![]() 交于点
交于点![]() ,连接
,连接![]() ,根据线面平行的性质得到
,根据线面平行的性质得到![]() ,又因为
,又因为![]() 为
为![]() 的中点,所以
的中点,所以![]() 为
为![]() 的中点,即可得到
的中点,即可得到![]() 的值.
的值.
(2)在直角梯形![]() 中证得
中证得![]() ,根据勾股定理证得
,根据勾股定理证得![]() ,即证
,即证![]() 平面
平面![]() ,再过
,再过![]() 做
做![]() ,连接
,连接![]() ,
,![]() 为二面角
为二面角![]() 的平面角,求其正切值即可.
的平面角,求其正切值即可.
(1)
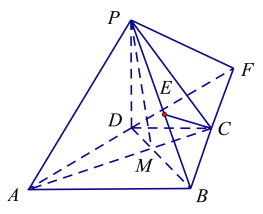
延长![]() ,
,![]() 交于点
交于点![]() ,连接
,连接![]() .
.
因为![]() ,
,![]() ,
,![]() ,
,
所以![]() ,即
,即![]() 为
为![]() 的中点.
的中点.
因为![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]()
所以![]() .
.
又因为![]() 为
为![]() 的中点,所以
的中点,所以![]() 为
为![]() 的中点.
的中点.
即![]() ,
,![]() .
.
(2)
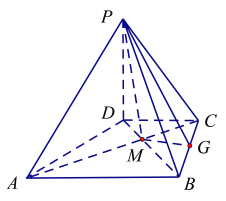
因为![]() ,
,![]()
所以在![]() 中,
中,![]() .
.
在![]() 中,
中,![]() .
.
又因为![]() ,
,![]() ,
,![]() ,
,
所以![]() .
.
因为![]() ,
,![]() ,
,
所以![]() ,
,![]() .
.
在![]() 中,
中,![]()
所以![]() .
.
在![]() 中,
中,![]() ,
,![]() ,
,![]()
![]() ,即
,即![]() .
.
因为平面![]() 平面
平面![]() ,
,![]() ,
,
所以![]() 平面
平面![]() .
.
过![]() 做
做![]() ,连接
,连接![]() .
.
因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() .
.
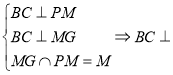 平面
平面![]() .
.
![]() 平面
平面![]() ,所以
,所以![]() .
.
所以![]() 为二面角
为二面角![]() 的平面角.
的平面角.
在![]() 中,
中,![]() ,
,
所以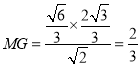 ,
,
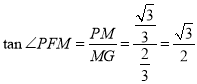 .
.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
【题目】诚信是立身之本,道德之基,我校学生会创设了“诚信水站”,既便于学生用水,又推进诚信教育,并用“![]() ”表示每周“水站诚信度”,为了便于数据分析,以四周为一周期,如表为该水站连续十二周(共三个周期)的诚信数据统计:
”表示每周“水站诚信度”,为了便于数据分析,以四周为一周期,如表为该水站连续十二周(共三个周期)的诚信数据统计:
第一周 | 第二周 | 第三周 | 第四周 | |
第一周期 |
|
|
|
|
第二周期 |
|
|
|
|
第三周期 |
|
|
|
|
(Ⅰ)计算表中十二周“水站诚信度”的平均数![]() ;
;
(Ⅱ)若定义水站诚信度高于![]() 的为“高诚信度”,
的为“高诚信度”,![]() 以下为“一般信度”则从每个周期的前两周中随机抽取两周进行调研,计算恰有两周是“高诚信度”的概率;
以下为“一般信度”则从每个周期的前两周中随机抽取两周进行调研,计算恰有两周是“高诚信度”的概率;
(Ⅲ)已知学生会分别在第一个周期的第四周末和第二个周期的第四周末各举行了一次“以诚信为本”的主题教育活动,根据已有数据,说明两次主题教育活动的宣传效果,并根据已有数据陈述理由.
