题目内容
如图,四棱锥S-ABCD 的底面是正方形,每条侧棱的长都是底面边长的 倍,P为侧棱SD上的点.
倍,P为侧棱SD上的点.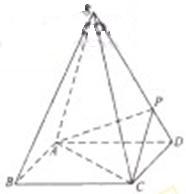
(Ⅰ)求证:AC⊥SD;
(Ⅱ)若SD⊥平面PAC,则侧棱SC上是否存在一点E,使得BE∥平面PAC。若存在,求SE:EC的值;若不存在,试说明理由.
(Ⅰ)只需证明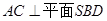 ;(Ⅱ)只需使得平面
;(Ⅱ)只需使得平面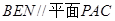
解析试题分析:解:(Ⅰ)连BD,设AC交BD于O,由题意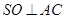 。在正方形ABCD中,
。在正方形ABCD中, ,所以
,所以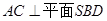 ,得
,得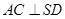 .………………4分
.………………4分
(Ⅱ) 在棱SC上存在一点E,使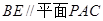
设正方形边长 ,则
,则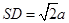 。
。
又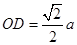 ,所以
,所以 ,
,
连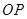 , 由
, 由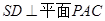 ,知
,知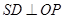 ,所以
,所以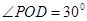 ,
,
则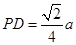 ,故可在
,故可在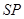 上取一点
上取一点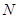 ,使
,使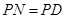 ,过
,过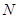 作
作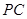 的平行线与
的平行线与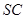 的交点即为
的交点即为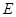 ,连BN。
,连BN。
在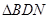 中知
中知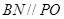 ,又由于
,又由于 ,故平面
,故平面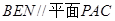 ,得
,得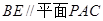 ,由于
,由于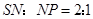 ,故
,故 .………………12分
.………………12分
考点:直线与平面垂直的判定定理;直线与平面平行的判定定理。
点评:结合定理可解决此题。但第二小题属于讨论题目,相对较难。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
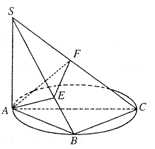
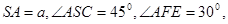 求三棱锥S—AEF的体积.
求三棱锥S—AEF的体积.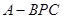 中,
中, ,
,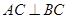 ,
, 为
为 中点,
中点,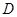 为
为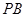 中点,且
中点,且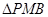 为正三角形.
为正三角形.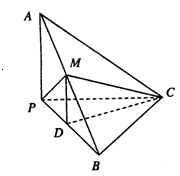
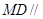 平面
平面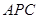 .
. ⊥平面
⊥平面

 ,底面
,底面 是正方形,
是正方形, 面
面 是
是 的中点,点
的中点,点 是
是 的中点,连接
的中点,连接 ,
,
 .
.
 面
面 ;
; ,
, ,求二面角
,求二面角 的余弦值.
的余弦值. 为底面的直棱柱被平面
为底面的直棱柱被平面 所截而得.
所截而得. 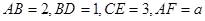 ,
, 为
为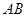 的中点.
的中点.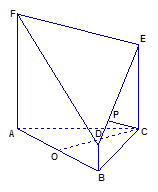
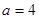 时,求平面
时,求平面 为何值时,在棱
为何值时,在棱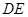 上存在点
上存在点 ,使
,使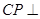 平面
平面 中,
中,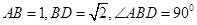 ,将它们沿对角线
,将它们沿对角线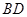 折起,折后的点
折起,折后的点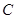 变为
变为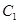 ,且
,且 .
.
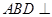 平面
平面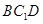 ;
;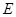 为线段
为线段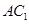 上的一个动点,当线段
上的一个动点,当线段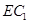 的长为多少时,
的长为多少时, 与平面
与平面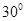 ?
? 中,底面ABCD是边长为1的正方形,
中,底面ABCD是边长为1的正方形, 平面ABCD,PA=AB,M,N分别为PB,AC的中点,
平面ABCD,PA=AB,M,N分别为PB,AC的中点, 