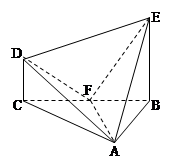题目内容
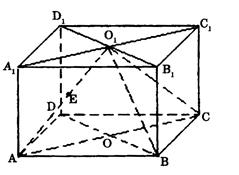
(本题满分12分)在正四棱柱ABCD-A1B1C1D1中,E为CC1的中点.
(1)求证:AC1∥平面BDE;(2)求异面直线A1E与BD所成角。
(1)连结AC交BD于O,连接EO因为平行四边形ABCD,
由OE为△AC1C中位线,得出OE∥AC1;从而AC1∥面BDE。
(2)先证BD⊥面A1AC C1
证得BD⊥A1E,A1E与BD所成角为900。
解析试题分析:(1)连结AC交BD于O,连接EO因为平行四边形ABCD, B
所以O为BD中点,E为CC1中点
所以OE为△AC1C中位线,
所以OE∥AC1-----------3
OE 面BDE
面BDE
AC1 面BDE
面BDE
AC1∥面BDE------------6
(2)因正四棱柱ABCD-A1B1C1D1
所以BD⊥A1A,又因BD⊥AC
A1A∩AC="A" ,A1A  面A1AC C1
面A1AC C1
AC 面A1AC C1
面A1AC C1
A1E
 面A1AC C1
面A1AC C1所以BD⊥A1E-
A1E与BD所成角为900------12
考点:本题主要考查立体几何的线面垂直,异面直线所成角的计算,几何体的特征。
点评:本题通过考查直线与平面的垂直关系及异面直线所成角的计算,考查空间想像能力、推理论证能力、运算求解能力、考查化归与转化思想,函数与方程思想等.本题中异面直线所成角的确定,通过证明线面垂直完成,值得深思。属中档题。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
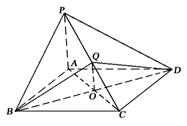
 平面O1BD
平面O1BD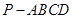 中,
中,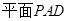
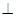 平面
平面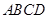 ,底面
,底面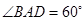 .
.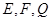 分别是
分别是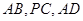 的中点.
的中点.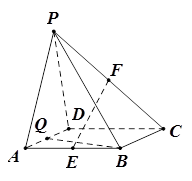
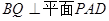 ;
;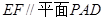 .
.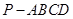 中,底面
中,底面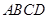 是正方形,侧面
是正方形,侧面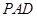 是正三角形,且平面
是正三角形,且平面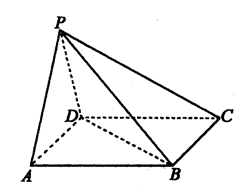
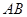 ⊥平面
⊥平面 与底面
与底面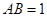 ,求点
,求点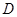 到平面
到平面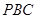 的距离.
的距离. 倍,P为侧棱SD上的点.
倍,P为侧棱SD上的点.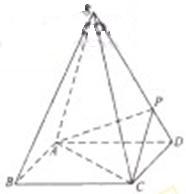
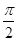 ,DC⊥平面ABC,EB⊥平面ABC,F是BC的中点,AB=AC=BE=2,CD=1
,DC⊥平面ABC,EB⊥平面ABC,F是BC的中点,AB=AC=BE=2,CD=1