题目内容
【题目】甲,乙两人进行射击比赛,各射击![]() 局,每局射击
局,每局射击![]() 次,射击中目标得
次,射击中目标得![]() 分,未命中目标得
分,未命中目标得![]() 分,两人
分,两人![]() 局的得分情况如下:
局的得分情况如下:
甲 |
|
|
|
|
乙 |
|
|
|
|
(1)若从甲的![]() 局比赛中,随机选取
局比赛中,随机选取![]() 局,求这
局,求这![]() 局的得分恰好相等的概率;
局的得分恰好相等的概率;
(2)从甲,乙两人的![]() 局比赛中随机各选取
局比赛中随机各选取![]() 局,记这
局,记这![]() 局的得分和为
局的得分和为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
【答案】(1)![]() ;(2)分布列见解析,
;(2)分布列见解析,![]()
【解析】
(1)求出基本事件总数![]() ,这2局的得分恰好相等包含的基本事件个数
,这2局的得分恰好相等包含的基本事件个数![]() .由此能求出这2局的得分恰好相等的概率
.由此能求出这2局的得分恰好相等的概率![]() ;
;
(2)甲,乙两人的4局比赛中随机各选取1局,记这2局的得分和为X,分别求出相应的概率,由此能求出X的分布列和数学期望.
解:(1)从甲的4局比赛中,随机选取2局,
基本事件总数![]() ,
,
这2局的得分恰好相等包含的基本事件个数![]() .
.
∴这2局的得分恰好相等的概率![]() ;
;
(2)甲,乙两人的4局比赛中随机各选取1局,记这2局的得分和为X,
则X的可能取值为13,15,16,18,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴X的分布列为: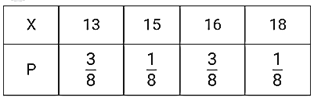
∴X的数学期望为![]() .
.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案
相关题目
【题目】根据国家统计局数据,1978年至2018年我国GDP总量从0.37万亿元跃升至90万亿元,实际增长了242倍多,综合国力大幅提升.
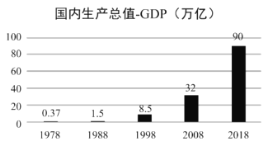
将年份1978,1988,1998,2008,2018分别用1,2,3,4,5代替,并表示为![]() ;
;![]() 表示全国GDP总量,表中
表示全国GDP总量,表中![]() ,
,![]() .
.
|
|
|
|
|
|
3 | 26.474 | 1.903 | 10 | 209.76 | 14.05 |
(1)根据数据及统计图表,判断![]() 与
与![]() (其中
(其中![]() 为自然对数的底数)哪一个更适宜作为全国GDP总量
为自然对数的底数)哪一个更适宜作为全国GDP总量![]() 关于
关于![]() 的回归方程类型?(给出判断即可,不必说明理由),并求出
的回归方程类型?(给出判断即可,不必说明理由),并求出![]() 关于
关于![]() 的回归方程.
的回归方程.
(2)使用参考数据,估计2020年的全国GDP总量.
线性回归方程![]() 中斜率和截距的最小二乘法估计公式分别为:
中斜率和截距的最小二乘法估计公式分别为:
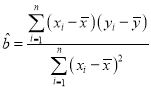 ,
,![]() .
.
参考数据:
| 4 | 5 | 6 | 7 | 8 |
| 55 | 148 | 403 | 1097 | 2981 |