Question

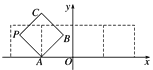
【题目】如图，直角梯形与等腰直角三角形所在的平面互相垂直．，，，.

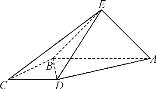
(1) 求证：；

(2) 求直线与平面所成角的正弦值；

(3) 线段上是否存在点，使平面若存在，求出；若不存在，说明理由．

Answer 1

【答案】（1）证明见解析；（2）；（3）线段上存在点，使得平面，且.

【解析】

（1）取AB中点O，连接EO，DO．利用等腰三角形的性质，可得EO⊥AB，证明边形OBCD为正方形，可得AB⊥OD，利用线面垂直的判定可得AB⊥平面EOD，从而可得AB⊥ED；

（2）由平面ABE⊥平面ABCD，且EO⊥AB，可得EO⊥平面ABCD，从而可得EO⊥OD．建立空间直角坐标系，确定平面ABE的一个法向量为，，利用向量的夹角公式，可求直线EC与平面ABE所成的角；

（3）存在点F，且时，有EC∥平面FBD．确定平面FBD的法向量，证明=0即可．

（1）证明：取AB中点O，连接EO，DO．

因为EB=EA，所以EO⊥AB．

因为四边形ABCD为直角梯形，AB=2CD=2BC，AB⊥BC，

所以四边形OBCD为正方形，所以AB⊥OD

因为EO∩OD=O

所以AB⊥平面EOD

因为ED平面EOD

所以AB⊥ED．

（2）解：因为平面ABE⊥平面ABCD，且 EO⊥AB，平面ABE∩平面ABCD=AB

所以EO⊥平面ABCD，

因为OD平面ABCD，所以EO⊥OD．

由OB，OD，OE两两垂直，建立如图所示的空间直角坐标系O﹣xyz．

因为△EAB为等腰直角三角形，所以OA=OB=OD=OE，设OB=1，所以O（0，0，0），A（﹣1，0，0），B（1，0，0），C（1，1，0），D（0，1，0），E（0，0，1）．

所以，平面ABE的一个法向量为．

设直线EC与平面ABE所成的角为θ，

所以 ，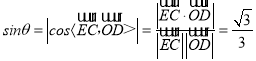

即直线EC与平面ABE所成角的正弦值为．

（3）解：存在点F，且时，有EC∥平面FBD．证明如下：由 ，，所以．

设平面FBD的法向量为=（a，b，c），则有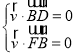

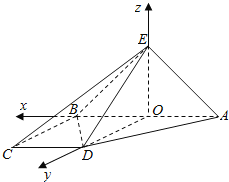
所以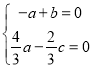取a=1，得=（1，1，2）．

因为=（1，1，﹣1）（1，1，2）=0，且EC平面FBD，所以EC∥平面FBD．

即点F满足时，有EC∥平面FBD．