Question

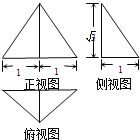
【题目】一个几何体的三视图如图所示，其中正视图是一个正三角形，则这个几何体的体积是 ，表面积是 ．

Answer 1

【答案】，+1+．

【解析】

试题分析：由三视图可知：该几何体是如图所示的三棱锥，其中侧面PAC⊥面ABC，△PAC是边长为2的正三角形，△ABC是边AC=2，边AC上的高OB=1，PO=为底面上的高．据此可计算出表面积和体积．

解：由三视图可知：该几何体是如图所示的三棱锥，

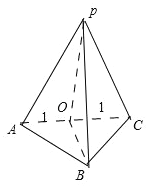
其中侧面PAC⊥面ABC，△PAC是边长为2的正三角形，△ABC是边AC=2，

边AC上的高OB=1，PO=为底面上的高．

于是此几何体的体积V=S△ABCPO=×2×1×=，

几何体的表面积

S=S△PAC+S△ABC+2S△PAB=××2+×2×1+2×××=+1+．

故答案为：，+1+．