题目内容
【题目】已知直线![]() 与抛物线
与抛物线![]() 相交于
相交于![]() 两点,点
两点,点![]() 是抛物线
是抛物线![]() 的准线与以
的准线与以![]() 为直径的圆的公共点,则下列结论正确的是( )
为直径的圆的公共点,则下列结论正确的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 的面积为
的面积为![]()
【答案】ABC
【解析】
由题意可知,抛物线![]() 的准线为
的准线为![]() ,利用抛物线的几何性质求出
,利用抛物线的几何性质求出![]() 和抛物线
和抛物线![]() 的方程和焦点坐标
的方程和焦点坐标![]() ,结合直线
,结合直线![]() 的方程可知,直线
的方程可知,直线![]() 经过焦点
经过焦点![]() ,利用抛物线的定义表示出以
,利用抛物线的定义表示出以![]() 为直径的圆的半径和圆心
为直径的圆的半径和圆心![]() ,由
,由![]() 得到关于
得到关于![]() 的方程,解方程求出
的方程,解方程求出![]() ,利用抛物线的定义和点到直线的距离分别求出
,利用抛物线的定义和点到直线的距离分别求出![]() 的长度和
的长度和![]() 的面积,据此即可判断.
的面积,据此即可判断.
由题意知,抛物线![]() 的准线为
的准线为![]() ,即
,即![]() ,解得
,解得![]() ,故选项A正确;
,故选项A正确;
因为![]() ,所以抛物线
,所以抛物线![]() 的方程为:
的方程为:![]() ,其焦点为
,其焦点为![]() ,
,
又直线![]() ,即
,即![]() ,所以直线
,所以直线![]() 恒过抛物线的焦点
恒过抛物线的焦点![]() ,
,
设点![]() ,因为
,因为![]() 两点在抛物线
两点在抛物线![]() 上,
上,
联立方程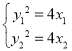 ,两式相减可得,
,两式相减可得,![]() ,
,
设![]() 的中点为
的中点为![]() ,则
,则![]() ,因为点
,因为点![]() 在直线
在直线![]() 上,
上,
解得可得![]() ,所以点
,所以点![]() 是以
是以![]() 为直径的圆的圆心,
为直径的圆的圆心,
由抛物线的定义知,圆![]() 的半径
的半径![]() ,
,
因为![]() ,所以
,所以![]() ,
,
解得![]() ,故选项B正确;
,故选项B正确;
因为![]() ,所以弦长
,所以弦长![]() ,故选项C正确;
,故选项C正确;
因为![]() ,所以直线
,所以直线![]() 为
为![]() ,由点到直线的距离公式可得,
,由点到直线的距离公式可得,
点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,所以
,所以![]() ,
,
故选项D错误;
故选:ABC

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目