题目内容
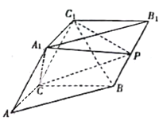
【题目】如图,在四棱锥![]() 中,
中,![]() 平面
平面![]() ,四边形
,四边形![]() 为平行四边形,且
为平行四边形,且![]() ,
,![]() .
.

(1)证明:![]() 平面
平面![]()
(2)当直线![]() 与平面
与平面![]() 所成角的正切值为
所成角的正切值为![]() 时,求锐二面角
时,求锐二面角![]() 的余弦值.
的余弦值.
【答案】(1)证明见解析(2)![]()
【解析】
(1)在四边形![]() 中,由平面几何知识,易证
中,由平面几何知识,易证![]() ,再由
,再由![]() 平面
平面![]() ,得到
,得到![]() ,根据线面垂直的判定定理证明
,根据线面垂直的判定定理证明![]() 平面
平面![]() .
.
(2)根据(1)知![]() 平面
平面![]() ,得到
,得到![]() 是直线
是直线![]() 与平面
与平面![]() 所成角,由直线
所成角,由直线![]() 与平面
与平面![]() 所成角的正切值为
所成角的正切值为![]() ,得到
,得到![]() ,从而
,从而![]() ,然后以A为原点,分别以AB,AC,在平面
,然后以A为原点,分别以AB,AC,在平面![]() 中,过A垂直于AB的直线为x,y,z轴建立空间直角坐标系,已知
中,过A垂直于AB的直线为x,y,z轴建立空间直角坐标系,已知![]() 是平面
是平面![]() 的一个法向量,再求得平面
的一个法向量,再求得平面![]() 的一个法向量,利用二面角的向量公式求解.
的一个法向量,利用二面角的向量公式求解.
(1)∵四边形![]() 为平行四边形,
为平行四边形,![]()
∴![]() ,
,![]() ,
,
∴在△![]() 中,由余弦定理得
中,由余弦定理得![]() ,
,
∴![]() .
.
∴![]() ,即
,即![]() ,
,
又∵![]() 平面
平面![]() ,∴
,∴![]() ,
,
又∵![]()
∴![]() 平面
平面![]()
(2)由(1)知,![]() 是直线
是直线![]() 与平面
与平面![]() 所成角,
所成角,![]() ,
,
∴![]() ,
,
又∵![]() 平面
平面![]() ,
,
∴![]()
∴△![]() 是等腰直角三角形,如图建立空间直角坐标系:
是等腰直角三角形,如图建立空间直角坐标系:

则有:![]() ,
,
由已知![]() 是平面
是平面![]() 的一个法向量,
的一个法向量,
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,![]() ,
,![]() ,
,
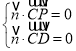 ,
,
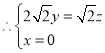 ,
,
![]()
 ,
,
∴锐二面角![]() 的余弦值
的余弦值![]()

 阅读快车系列答案
阅读快车系列答案【题目】为了解某地网民浏览购物网站的情况,从该地随机抽取100名网民进行调查,其中男性、女性人数分别为60和40.下面是根据调查结果统计的数据,将日均浏览购物网站时间不低于40分钟的网民称为“网购达人”,已知“网购达人”中女性人数为15人.
日均浏览购物网站时间(分钟) |
|
|
|
|
|
|
人数 | 2 | 14 | 24 | 35 | 20 | 5 |
(1)根据已知条件完成下面的![]() 列联表,并判断是否有99%的把握认为是否为“网购达人”与性别有关;
列联表,并判断是否有99%的把握认为是否为“网购达人”与性别有关;
非网购达人 | 网购达人 | 总计 | |
男 | |||
女 | 15 | ||
总计 |
(2)从上述调查中的“网购达人”中按性别分层抽样,抽取5人发放礼品,再从这5人中随机选出2人作为“最美网购达人”,求这两个“最美网购达人”中恰好为1男1女的概率.
参考公式: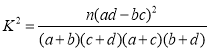 ,其中
,其中![]() .
.
参考数据:
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |