题目内容
如图,在棱长为a的正方体A1B1C1D1-ABCD中,(1)若以D为坐标原点,分别以DA,DC,DD1所在的直线为x轴、y轴、z轴,建立空间直角坐标系,试写出B,B1两点的坐标.
(2)证明B1D⊥面A1BC1;
(3)求线AC到面A1BC1的距离.

【答案】分析:(1)根据空间直角坐标系,写成点的坐标.(2)利用线面垂直的判定定理去证明线面垂直.(3)利用等积法求距离.
解答:解:(1)B(a,a,0)B1(a,a,a)
(2)易证A1C1⊥面DBB1D1,∴A1C1⊥B1D,同理可证A1B⊥B1D,
又A1C1∩A1B=A1,∴B1D⊥面A1BC1.
(3)∵AC∥A1C1,∴AC∥面A1BC1
∴线AC到面A1BC1的距离即为点A到面A1BC1的距离,也就是点B1到面A1BC1的距离,记为h,
在三棱锥B1-BA1C1中有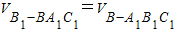 ,
,
即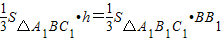 ,
,
∴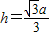 .
.
点评:本题主要考查空间线面垂直的判断和直线到平面的距离公式,综合性较强.
解答:解:(1)B(a,a,0)B1(a,a,a)
(2)易证A1C1⊥面DBB1D1,∴A1C1⊥B1D,同理可证A1B⊥B1D,
又A1C1∩A1B=A1,∴B1D⊥面A1BC1.
(3)∵AC∥A1C1,∴AC∥面A1BC1
∴线AC到面A1BC1的距离即为点A到面A1BC1的距离,也就是点B1到面A1BC1的距离,记为h,
在三棱锥B1-BA1C1中有
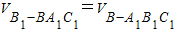 ,
,即
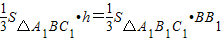 ,
,∴
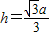 .
.点评:本题主要考查空间线面垂直的判断和直线到平面的距离公式,综合性较强.

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目
 如图,在棱长为2的正四面体A-BCD中,若以△ABC为视角正面,则其正视图的面积是( )
如图,在棱长为2的正四面体A-BCD中,若以△ABC为视角正面,则其正视图的面积是( ) ,当
,当 取什么位置时,三棱柱的体积最大?
取什么位置时,三棱柱的体积最大?





