题目内容
已知一条曲线C在y轴右边,C上每一点到点F(1,0)的距离减去它到y轴距离的差都是1
(1)求曲线C的方程.
(2)是否存在正数m,对于过点M(m,0)且与曲线C有两个交点A,B的任一直线,都有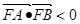 ?若存在,求出m的取值范围,若不存在,请说明理由.
?若存在,求出m的取值范围,若不存在,请说明理由.
(1)求曲线C的方程.
(2)是否存在正数m,对于过点M(m,0)且与曲线C有两个交点A,B的任一直线,都有
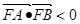 ?若存在,求出m的取值范围,若不存在,请说明理由.
?若存在,求出m的取值范围,若不存在,请说明理由.解:(Ⅰ)设P(x,y)是曲线C上任意一点,那么点P(x,y)满足:

化简得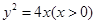 .
.
(Ⅱ)设过点M(m,0)(m>0)的直线l与曲线C的交点为A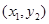 ,B
,B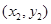 。
。
设l的方程为x=ty+m,由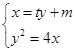 得
得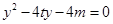 ,△=16(
,△=16(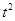 +m)>0,
+m)>0,
于是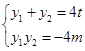 ①
①
又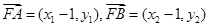 。
。
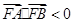
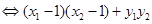 =
=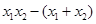 +1+
+1+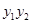 <0②
<0②
又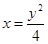 ,于是不等式②等价于
,于是不等式②等价于
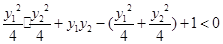
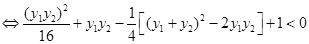 ③
③
由①式,不等式③等价于
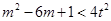 ④
④
对任意实数t,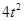 的最小值为0,所以不等式④对于一切t成立等价于
的最小值为0,所以不等式④对于一切t成立等价于
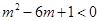 ,即
,即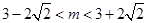 。
。
由此可知,存在正数m,对于过点M(m,0)且与曲线C有两个交点A,B的任一直线,都有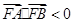 ,且m的取值范围
,且m的取值范围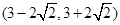 。
。

化简得
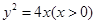 .
.(Ⅱ)设过点M(m,0)(m>0)的直线l与曲线C的交点为A
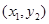 ,B
,B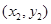 。
。设l的方程为x=ty+m,由
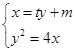 得
得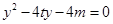 ,△=16(
,△=16(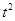 +m)>0,
+m)>0,于是
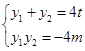 ①
①又
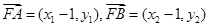 。
。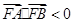
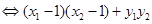 =
=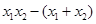 +1+
+1+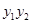 <0②
<0②又
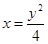 ,于是不等式②等价于
,于是不等式②等价于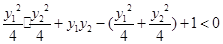
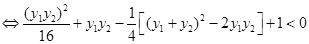 ③
③由①式,不等式③等价于
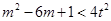 ④
④对任意实数t,
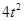 的最小值为0,所以不等式④对于一切t成立等价于
的最小值为0,所以不等式④对于一切t成立等价于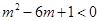 ,即
,即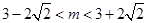 。
。由此可知,存在正数m,对于过点M(m,0)且与曲线C有两个交点A,B的任一直线,都有
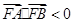 ,且m的取值范围
,且m的取值范围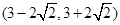 。
。(1)由题意知曲线C上的点到F(1,0)的距离与到直线x=-1的距离相等.
可确定其轨迹是抛物线,即可求出其方程为y2=4x.
(2)设过点M的直线方程为x=ty+m,然后与抛物线方程联立,消去x,利用韦达定理表示出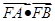 ,再证明其小于零即可.
,再证明其小于零即可.
可确定其轨迹是抛物线,即可求出其方程为y2=4x.
(2)设过点M的直线方程为x=ty+m,然后与抛物线方程联立,消去x,利用韦达定理表示出
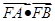 ,再证明其小于零即可.
,再证明其小于零即可.
练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
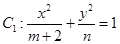 与双曲线
与双曲线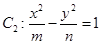 共焦点,则椭圆
共焦点,则椭圆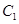 的离心率
的离心率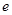 的取值范围为( )
的取值范围为( )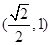

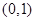

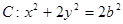 (常数
(常数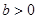 )的左右焦点分别为
)的左右焦点分别为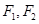 ,
,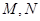 是直线
是直线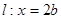 上的两个动点,
上的两个动点,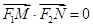 .
.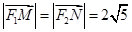 ,求
,求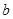 的值;
的值;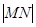 的最小值.
的最小值.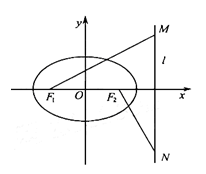
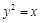 有且仅有一个公共点,并且过点
有且仅有一个公共点,并且过点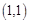 的直线方程为 .
的直线方程为 .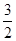 ),动圆P经过点F且和直线y=
),动圆P经过点F且和直线y=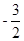 相切,记动圆的圆心P的轨迹为曲线W.
相切,记动圆的圆心P的轨迹为曲线W. ,
, ,分别交曲线W于A,B和C,D.①求四边形ABCD面积的最小值;②分别在A,B两点作曲线W的切线,这两条切线的交点记为Q,求证:QA⊥QB,且点Q在某一定直线上。
,分别交曲线W于A,B和C,D.①求四边形ABCD面积的最小值;②分别在A,B两点作曲线W的切线,这两条切线的交点记为Q,求证:QA⊥QB,且点Q在某一定直线上。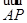 ·
·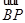 =k|
=k|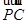 |2.
|2.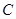 :
: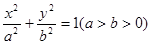 的右焦点
的右焦点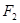 引直线
引直线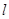 ,与
,与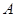 点,与
点,与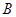 、
、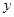 轴交于
轴交于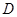 点,若
点,若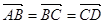 ,则
,则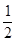
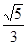
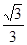
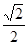 .
.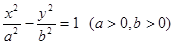 的离心率
的离心率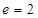 ,右焦点
,右焦点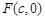 ,方程
,方程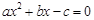 的两个根分别为
的两个根分别为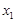 ,
,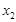 ,则点
,则点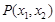 在
在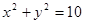 内
内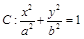
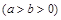 的离心率为
的离心率为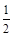 ,以原点为圆心,椭圆的短半轴为半径的圆与直线
,以原点为圆心,椭圆的短半轴为半径的圆与直线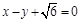 相切.
相切.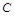 的方程;
的方程;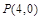 ,
,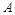 ,
,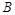 是椭圆
是椭圆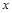 轴对称的任意两个不同的点,连结
轴对称的任意两个不同的点,连结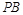 交椭圆
交椭圆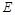 ,证明直线
,证明直线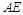 与
与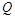 ;
;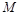 ,
,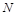 两点,求
两点,求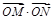 的取值范围.
的取值范围.