题目内容
1.设A,B分别为椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)和双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的公共顶点,P,M分别为双曲线和椭圆上异于A,B的两动点,且满足$\overline{AP}$+$\overline{BP}$=$λ(\overline{AM}+\overline{BM})$,其中λ∈R,|λ|>1,设直线AP,BP,AM,BM的斜率分别为k1,k2,k3,k4且k1+k2=5,则k3+k4=-5.分析 如图所示,由满足$\overline{AP}$+$\overline{BP}$=$λ(\overline{AM}+\overline{BM})$,其中λ∈R,|λ|>1,利用向量的平行四边形法则可得:O,M,P三点共线.设P(x1,y1),M(x2,y2),$\frac{{y}_{1}}{{x}_{1}}=\frac{{y}_{2}}{{x}_{2}}$=k≠0.分别利用点在双曲线与椭圆上可得$\frac{{x}_{1}^{2}-{a}^{2}}{{a}^{2}}$=$\frac{{y}_{1}^{2}}{{b}^{2}}$,$\frac{{x}_{2}^{2}-{a}^{2}}{{a}^{2}}$=-$\frac{{y}_{2}^{2}}{{b}^{2}}$.k1+k2=5,利用斜率计算公式可得5=$\frac{2{b}^{2}}{{a}^{2}}•\frac{1}{k}$.再利用向量计算公式即可得出k3+k4.
解答 解:如图所示,
∵满足$\overline{AP}$+$\overline{BP}$=$λ(\overline{AM}+\overline{BM})$,其中λ∈R,|λ|>1,
∴-2$\overrightarrow{PO}$=λ•(-2$\overrightarrow{MO}$),
∴O,M,P三点共线.
设P(x1,y1),M(x2,y2),$\frac{{y}_{1}}{{x}_{1}}=\frac{{y}_{2}}{{x}_{2}}$=k≠0.
则$\frac{{x}_{1}^{2}}{{a}^{2}}$-$\frac{{y}_{1}^{2}}{{b}^{2}}$=1,$\frac{{x}_{2}^{2}}{{a}^{2}}$+$\frac{{y}_{2}^{2}}{{b}^{2}}$=1,
∴$\frac{{x}_{1}^{2}-{a}^{2}}{{a}^{2}}$=$\frac{{y}_{1}^{2}}{{b}^{2}}$,$\frac{{x}_{2}^{2}-{a}^{2}}{{a}^{2}}$=-$\frac{{y}_{2}^{2}}{{b}^{2}}$,
∵k1+k2=5,
∴5=$\frac{{y}_{1}}{{x}_{1}+a}$+$\frac{{y}_{1}}{{x}_{1}-a}$=$\frac{2{x}_{1}{y}_{1}}{{x}_{1}^{2}-{a}^{2}}$=$\frac{2{x}_{1}{y}_{1}}{\frac{{{a}^{2}y}_{1}^{2}}{{b}^{2}}}$=$\frac{2{b}^{2}}{{a}^{2}}•\frac{1}{k}$.
∴k3+k4=$\frac{{y}_{2}}{{x}_{2}+a}+\frac{{y}_{2}}{{x}_{2}-a}$=$\frac{2{x}_{2}{y}_{2}}{{x}_{2}^{2}-{a}^{2}}$=-$\frac{2{b}^{2}}{{a}^{2}}$$•\frac{1}{k}$=-5.
故答案为:-5.
点评 本题考查了椭圆与双曲线的标准方程及其性质、向量的平行四边形法则、斜率计算公式,考查了推理能力与计算能力,属于难题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
| A. | 14π | B. | 12π | C. | 8π | D. | 16π |
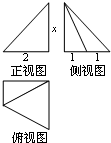 某几何体的三视图如图所示,且该几何体的体积是6,则正视图中的x的值是( )
某几何体的三视图如图所示,且该几何体的体积是6,则正视图中的x的值是( )| A. | 9 | B. | 8 | C. | 3 | D. | 6 |
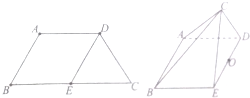 如图,ABCD为等腰梯形,且AD∥BC,E为BC的中点,AB=AD=BE,沿DE将△CDE折起成四棱锥C-ABED.
如图,ABCD为等腰梯形,且AD∥BC,E为BC的中点,AB=AD=BE,沿DE将△CDE折起成四棱锥C-ABED.