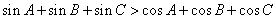题目内容
已知 均为正数,证明:
均为正数,证明: ,并确定
,并确定 为何值时,等号成立。
为何值时,等号成立。
利用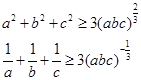 ①所以
①所以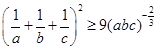 ② ……6分
② ……6分
故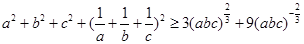 .
.
又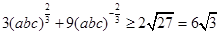 ③
③
(证法二)利用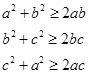 证明。
证明。
解析试题分析:(证法一)因为a,b,c均为正数,由平均值不等式得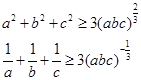 ①所以
①所以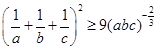 ② ……6分
② ……6分
故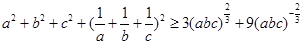 .
.
又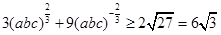 ③
③
所以原不等式成立. ……8分
当且仅当a=b=c时,①式和②式等号成立。当且仅当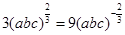 时,③式等号成立。即当且仅当a=b=c=
时,③式等号成立。即当且仅当a=b=c=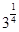 时,原式等号成立。 ……10分
时,原式等号成立。 ……10分
(证法二)因为a,b,c均为正数,由基本不等式得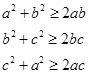
所以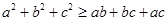 ①
①
同理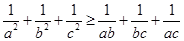 ② ……6分
② ……6分
故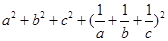
 ③
③
所以原不等式成立. ……8分
当且仅当a=b=c时,①式和②式等号成立,当且仅当a=b=c,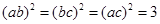 时,③式等号成立。
时,③式等号成立。
即当且仅当a=b=c=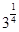 时,原式等号成立。 ……10分
时,原式等号成立。 ……10分
考点:本题主要考查简单不等式的证明。
点评:中档题,不等式的证明方法,通常有“综合法”、“分析法”“反证法”等,不等式的性质、基本不等式等基础知识,是不等式证明的基础,应牢记并灵活运用。本题证法较多,入口较易。

练习册系列答案
相关题目
关于 的不等式
的不等式 (
( )的解集为
)的解集为 ,且
,且 ,则
,则 ( )
( )
A.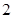 | B. | C.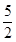 | D. |
(5分)(2011•广东)不等式2x2﹣x﹣1>0的解集是( )
A. | B.(1,+∞) | C.(﹣∞,1)∪(2,+∞) | D. ∪(1,+∞) ∪(1,+∞) |
已知 ,则“
,则“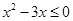 ”是“
”是“ 成立”的( )
成立”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
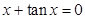 的正根从小到大地依次排列为
的正根从小到大地依次排列为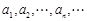 ,
,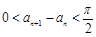 ; ②
; ②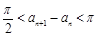 ;
;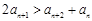 ; ④
; ④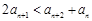 ;
;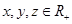 ,
,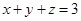 .
.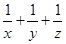 的最小值;
的最小值;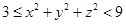 .
.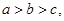 求证:
求证: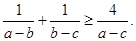
 的一个近似值,令
的一个近似值,令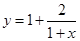 .
. ;
;