题目内容
在锐角三角形ABC中,求证: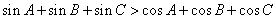
证明三角不等式,关键是能通过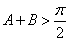 ,进而得到
,进而得到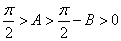 ,结合三角函数性质得到不等式。
,结合三角函数性质得到不等式。
解析试题分析:∵在锐角三角形ABC中,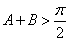 ,∴
,∴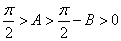 ,
,
∵在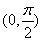 内正弦函数单调递增,∴
内正弦函数单调递增,∴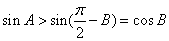 ,即
,即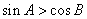 同理,
同理, ,
,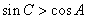 ∴
∴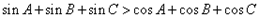
考点:证明三角不等式
点评:解决的关键是对于三角形中角的不等式关系,结合三角函数单调性得到三角不等式,属于基础题。

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
已知 ,如果
,如果 是
是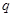 的充分不必要条件,则实数k的取值范围是( )
的充分不必要条件,则实数k的取值范围是( )
A. | B. | C. | D. |
已知关于x的不等式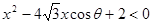 与
与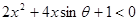 的解集,分别是
的解集,分别是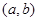 和
和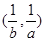 ,且
,且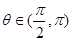 ,则
,则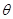 的值是( ).
的值是( ).
A.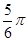 | B.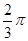 | C.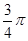 | D.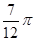 . . |
若不等式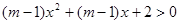 的解集是R,则m的范围是( )
的解集是R,则m的范围是( )
A.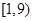 |
B. |
C.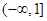 |
D. |
 、
、 、
、 按从小到大排列为 .
按从小到大排列为 . 证明
证明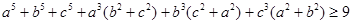 。
。 均为正数,证明:
均为正数,证明: ,并确定
,并确定 ,不等式
,不等式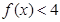 的解集为
的解集为
 时,证明:
时,证明: