题目内容
关于 的不等式
的不等式 (
( )的解集为
)的解集为 ,且
,且 ,则
,则 ( )
( )
A.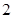 | B. | C.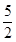 | D. |
A.
解析试题分析:由题意可知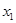 ,
,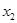 为一元二次方程
为一元二次方程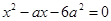 的两根,∴
的两根,∴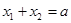 ,
,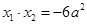 ,
,
∴ ,即
,即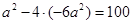 ,又∵
,又∵ ,∴
,∴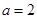 .
.
考点:一元二次不等式与韦达定理结合.

练习册系列答案
相关题目
已知 ,如果
,如果 是
是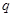 的充分不必要条件,则实数k的取值范围是( )
的充分不必要条件,则实数k的取值范围是( )
A. | B. | C. | D. |
不等式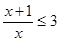 的解集是( )
的解集是( )
A. | B.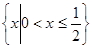 |
C.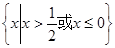 | D. |
已知关于x的不等式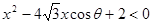 与
与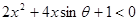 的解集,分别是
的解集,分别是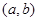 和
和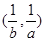 ,且
,且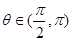 ,则
,则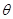 的值是( ).
的值是( ).
A.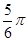 | B.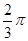 | C.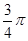 | D.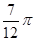 . . |
在 上定义运算
上定义运算 :
: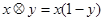 ,若不等式
,若不等式 对任意实数
对任意实数 都成立,则
都成立,则 的取值范围是( )
的取值范围是( )
A. | B. | C. | D.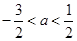 |
若关于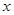 的方程
的方程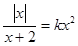 有四个不同的实数解,则实数
有四个不同的实数解,则实数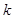 的取值范围为()
的取值范围为()
A. | B. | C.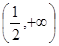 | D. |
“0<a<1”是“ax2+2ax+1>0的解集是实数集R”的( )
| A.充分而不必要条件 |
| B.必要而不充分条件 |
| C.充要条件 |
| D.既不充分也不必要条件 |
 ;
; 恒成立的k的最大值.
恒成立的k的最大值. 均为正数,证明:
均为正数,证明: ,并确定
,并确定