题目内容
【题目】已知函数
在
处的切线斜率为
.
（1）若函数
在
上单调，求实数
的最大值；
（2）当
时，若存在不等的
使得
，求实数
的取值范围.
【答案】（1）
；（2）
.
【解析】
(1)先根据切线的斜率求出
，再根据函数单调，得到
恒成立，求出b的最大值.(2)转化为存在不等的
，且
使得
，得函数
在上单调递增.结合（1）进而得到k＞0.
（1）函数
在
处的切线斜率为
解得.
所以
，故
因为函数
在
上单调
故
或
在上恒成立.
显然
即在上不恒成立.
所以恒成立即可.
因为
可知
在
上单减，单增
故
，所以实数
的最大值为1.
（2）当
时，由（1）知函数在上单调递增
不妨设
，使得
即为存在不等的，且使得
.
其否定为：任意，都有
即：函数
在上单调递增.
由（1）知：
即
所以若存在不等的使得
实数
的取值范围为.
【题目】“大众创业,万众创新”是李克强总理在本届政府工作报告中向全国人民发出的口号.某生产企业积极响应号召,大力研发新产品,为了对新研发的一批产品进行合理定价,将该产品按事先拟定的价格进行试销,得到一组销售数据
,如表所示：
试销单价x(元) | 4 | 5 | 6 | 7 | 8 |
产品销量y(件) | q | 85 | 82 | 80 | 75 |
已知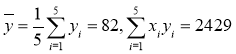
（1）求出q的值；
（2）已知变量
具有线性相关关系,求产品销量y（件）关于试销单价x（元）的线性回归方程
；
（3）假设试销单价为10元,试估计该产品的销量.
【题目】某种产品的广告费支出x（单位：百万元）与销售额y（单位：百万元）之间有如下的对应数据：
x | 2 | 4 | 5 | 6 | 8 |
y | 30 | 40 | 60 | 50 | 70 |
（1）画出散点图；
（2）求y关于x的线性回归方程.
（3）如果广告费支出为一千万元，预测销售额大约为多少百万元？
参考公式用最小二乘法求线性回归方程系数公式：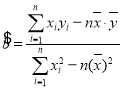
，
.
【题目】某行业主管部门为了解本行业中小企业的生产情况，随机调查了100个企业，得到这些企业第一季度相对于前一年第一季度产值增长率y的频数分布表.
|
|
|
|
|
|
企业数 | 2 | 24 | 53 | 14 | 7 |
（1）分别估计这类企业中产值增长率不低于40%的企业比例、产值负增长的企业比例；
（2）求这类企业产值增长率的平均数与标准差的估计值（同一组中的数据用该组区间的中点值为代表）.（精确到0.01）
附：
.