题目内容
【题目】随着经济模式的改变,微商和电商已成为当今城乡一种新型的购销平台.已知经销某种商品的电商在任何一个销售季度内,每售出![]() 吨该商品可获利润
吨该商品可获利润![]() 万元,未售出的商品,每
万元,未售出的商品,每![]() 吨亏损
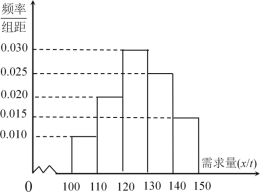
吨亏损![]() 万元.根据往年的销售经验,得到一个销售季度内市场需求量的频率分布直方图如图所示.已知电商为下一个销售季度筹备了
万元.根据往年的销售经验,得到一个销售季度内市场需求量的频率分布直方图如图所示.已知电商为下一个销售季度筹备了![]() 吨该商品.现以
吨该商品.现以![]() (单位:吨,
(单位:吨,![]() )表示下一个销售季度的市场需求量,
)表示下一个销售季度的市场需求量,![]() (单位:万元)表示该电商下一个销售季度内经销该商品获得的利润.
(单位:万元)表示该电商下一个销售季度内经销该商品获得的利润.
(1)将![]() 表示为
表示为![]() 的函数,求出该函数表达式;
的函数,求出该函数表达式;
(2)根据直方图估计利润![]() 不少于57万元的概率;
不少于57万元的概率;
(3)根据频率分布直方图,估计一个销售季度内市场需求量![]() 的平均数与中位数的大小(保留到小数点后一位).
的平均数与中位数的大小(保留到小数点后一位).
【答案】(1)![]() ;(2)0.7;(3)平均数为
;(2)0.7;(3)平均数为![]() (吨),估计中位数应为
(吨),估计中位数应为![]() (吨)
(吨)
【解析】
(1)分别计算![]() 和
和![]() 时T的值,用分段函数表示T的解析式;
时T的值,用分段函数表示T的解析式;
(2)计算利润T不少于57万元时x的取值范围,求出对应的频率值即可;
(3)利用每一小组底边的中点乘以对应的矩形的面积(即频率)求和得出平均数,根据中位数两边频率相等(即矩形面积和相等)求出中位数的大小.
解:(1)当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ,
,
所以,![]() ;
;
(2)根据频率分布直方图及(1)知,
当![]() 时,由
时,由![]() ,得
,得![]() ,
,
当![]() 时,由
时,由![]()
所以,利润![]() 不少于57万元当且仅当
不少于57万元当且仅当![]() ,
,
于是由频率分布直方图可知市场需求量![]() 的频率为
的频率为
![]() ,
,
所以下一个销售季度内的利润![]() 不少于57万元的概率的估计值为0.7;
不少于57万元的概率的估计值为0.7;
(3)估计一个销售季度内市场需求量![]() 的平均数为
的平均数为
![]()
![]() (吨)
(吨)
由频率分布直方图易知,
由于![]() 时,对应的频率为
时,对应的频率为![]() ,
,
而![]() 时,对应的频率为
时,对应的频率为![]() ,
,
因此一个销售季度内市场需求量![]() 的中位数应属于区间
的中位数应属于区间![]() ,于是估计中位数应为
,于是估计中位数应为![]() (吨).
(吨).

【题目】对某产品1到6月份销售量及其价格进行调查,其售价x和销售量y之间的一组数据如下表所示:
月份i | 1 | 2 | 3 | 4 | 5 | 6 |
单价 | 9 | 9.5 | 10 | 10.5 | 11 | 8 |
销售量 | 11 | 10 | 8 | 6 | 5 | 14 |
(1)根据1至5月份的数据,求出y关于x的回归直线方程;
(2)若由回归直线方程得到的估计数据与剩下的检验数据的误差不超过0.5元,则认为所得到的回归直线方程是理想的,试问所得到的回归直线方程是否理想?
(3)预计在今后的销售中,销售量与单价仍然服从(1)中的关系,且该产品的成本是2.5元/件,为获得最大利润,该产品的单价应定为多少元?