Question

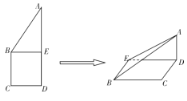
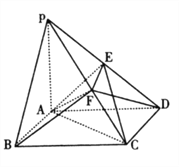
【题目】如图，在五面体中，四边形为矩形， 为等边三角形，且平面平面， .

（1）证明：平面平面；

（2）若，求二面角的余弦值.

Answer 1

【答案】（1）见解析；（2）

【解析】试题分析：

(1)取DE中点G，于是AG⊥DE，由面面垂直的性质定理可得AG⊥面CDEF，则AG⊥DC，又CD⊥AD，由线面垂直的判断定理可得CD⊥面ADE，即面ADE⊥面ABCD．

(2)取AD中点O，以O为坐标原点，OA、OE为x、z轴建系．由题意可得：平面FBC的法向量为，平面BCD的法向量为，则二面角F-BC-D的余弦值为．

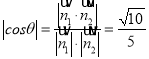试题解析：

（1）证明：取DE中点G，于是AG⊥DE，

又面ADE⊥面CDEF，且面ADE∩面CDEF=DE，所以AG⊥面CDEF，

则AG⊥DC，又CD⊥AD，所以CD⊥面ADE，

即面ADE⊥面ABCD．

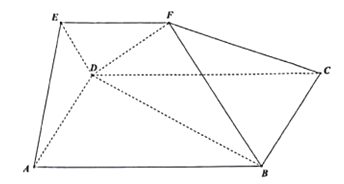
（2）解：取AD中点O，于是EO⊥面ABCD，所以，如图：

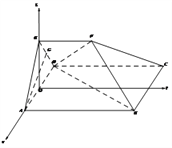
以O为坐标原点，OA、OE为x、z轴建系．设OA长度为1，

于是点坐标为： ，

因为CD∥AB，所以AB∥平面CDEF，又平面ABEF∩平面CDEF=EF，则EF∥AB；

所以设，所以点．

那么，由于BF⊥DF，

所以，解得．于是，

进而面FBC的法向量为，

又面BCD的法向量为，记二面角F-BC-D为，所以

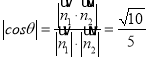，又因为是锐角，所以二面角F-BC-D的余弦值为．