Question

【题目】.已知函数.

（1）求过点的图象的切线方程；

（2）若函数存在两个极值点， ，求的取值范围；

（3）当时，均有恒成立，求的取值范围.

Answer 1

【答案】(1) (2) （3）

【解析】试题分析：（1）设切点坐标为，则切线方程为 ，根据点坐标，即可求出，从而得到切线方程；（2）对求导，令，要使存在两个极值点， ，则方程有两个不相等的正数根，从而只需满足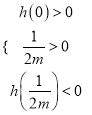即可；（3）由在上恒成立可得在上恒成立，令，求出的单调性，可得出的最大值，即可求得的取值范围.

试题解析：（1）由题意得，函数的定义域为，

设切点坐标为，则切线方程为

把点代入切线方程，得： ，

过点的切线方程为：

（2）∵

∴

令

要使存在两个极值点， ，则方程有两个不相等的正数根.

又， .

故只需满足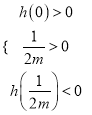即可

解得：

（3）由于在上恒成立.

∴在上恒成立.

令

则

当时，

令，则

在上单调递增

又，

∴存在便得，即，

故当时， ，此时

当时， 此时.

故函数在上递增，在上递减

从而：

令，

则

在上单调递增，

∴

故.