题目内容
已知数列{an},an∈N*,前n项和Sn= (an+2)2.
(an+2)2.
(1)求证:{an}是等差数列;
(2)若bn= an﹣30,求数列{bn}的前n项和的最小值.
an﹣30,求数列{bn}的前n项和的最小值.
 (an+2)2.
(an+2)2.(1)求证:{an}是等差数列;
(2)若bn=
 an﹣30,求数列{bn}的前n项和的最小值.
an﹣30,求数列{bn}的前n项和的最小值.解:(1)证明:∵an+1
=Sn+1﹣Sn
= (an+1+2)2﹣
(an+1+2)2﹣ (an+2)2,
(an+2)2,
∴8an+1=(an+1+2)2﹣(an+2)2,
∴(an+1﹣2)2﹣(an+2)2=0,(an+1+an)(an+1﹣an﹣4)=0.
∵an∈N*,∴an+1+an≠0,
∴an+1﹣an﹣4=0.
即an+1﹣an=4,∴数列{an}是等差数列.
(2)由(1)知a1=S1= (a1+2),解得a1=2.∴an=4n﹣2,
(a1+2),解得a1=2.∴an=4n﹣2,
bn= an﹣30=2n﹣31,(以下用两种方法求解)
an﹣30=2n﹣31,(以下用两种方法求解)
法一:
由bn=2n﹣31可得:首项b1=﹣29,公差d=2
∴数列{bn}的前n项和sn=n2﹣30n=(n﹣15)2﹣225
∴当n=15时,sn=225为最小;
法二:
由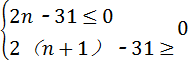 得
得
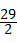 ≤n<
≤n<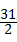 .∵n∈N*,∴n=15,
.∵n∈N*,∴n=15,
∴{an}前15项为负值,以后各项均为正值.
∴S5最小.又b1=﹣29,
∴S15= =﹣225
=﹣225
=Sn+1﹣Sn
=
 (an+1+2)2﹣
(an+1+2)2﹣ (an+2)2,
(an+2)2,∴8an+1=(an+1+2)2﹣(an+2)2,
∴(an+1﹣2)2﹣(an+2)2=0,(an+1+an)(an+1﹣an﹣4)=0.
∵an∈N*,∴an+1+an≠0,
∴an+1﹣an﹣4=0.
即an+1﹣an=4,∴数列{an}是等差数列.
(2)由(1)知a1=S1=
 (a1+2),解得a1=2.∴an=4n﹣2,
(a1+2),解得a1=2.∴an=4n﹣2,bn=
 an﹣30=2n﹣31,(以下用两种方法求解)
an﹣30=2n﹣31,(以下用两种方法求解)法一:
由bn=2n﹣31可得:首项b1=﹣29,公差d=2
∴数列{bn}的前n项和sn=n2﹣30n=(n﹣15)2﹣225
∴当n=15时,sn=225为最小;
法二:
由
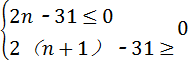 得
得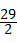 ≤n<
≤n<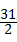 .∵n∈N*,∴n=15,
.∵n∈N*,∴n=15,∴{an}前15项为负值,以后各项均为正值.
∴S5最小.又b1=﹣29,
∴S15=
 =﹣225
=﹣225略

练习册系列答案
相关题目
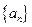 满足:
满足: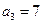 ,
,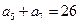 ,
,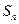 .
.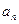 及
及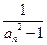 (
( ),求数列
),求数列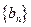 的前n项和
的前n项和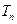 .
. 的公比为
的公比为 ,首项为
,首项为 ,其前
,其前 项的和为
项的和为 .数列
.数列 的前
的前 , 数列
, 数列 的前
的前
 ,
, ,求
,求 的通项公式;(Ⅱ)①当
的通项公式;(Ⅱ)①当 与
与 的大小; ②当
的大小; ②当 ,问是否存在常数
,问是否存在常数 (与n无关),使得等式
(与n无关),使得等式 恒成立,若存在,求出
恒成立,若存在,求出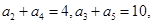 则它的前10项的和S10等于( )
则它的前10项的和S10等于( )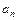 =1+
=1+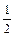 +
+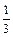 +…+
+…+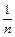 (n
(n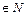 ),
),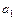 +
+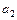 +…+
+…+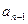 =g(n)(
=g(n)(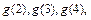 并猜想
并猜想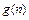 的表达式;
的表达式;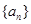 的前n项和为
的前n项和为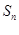 ,且
,且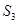 =6,
=6,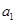 =4,则公差d等于
=4,则公差d等于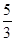
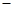 2
2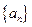 是公差不为零的等差数列,
是公差不为零的等差数列,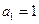 ,且
,且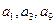 成等比数列.
成等比数列.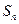 ;
;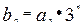 ,
, 求数列
求数列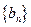 的前n项和
的前n项和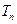
 满足
满足 则
则 ,
, ,……
,…… ,
, ,
, ,
, ,
,
 ,……则此数列中的2011项是
,……则此数列中的2011项是