题目内容
.(本小题满分14分)已知等比数列 的公比为
的公比为 ,首项为
,首项为 ,其前
,其前 项的和为
项的和为 .数列
.数列 的前
的前 项的和为
项的和为 , 数列
, 数列 的前
的前 项的和为
项的和为
(Ⅰ)若 ,
, ,求
,求 的通项公式;(Ⅱ)①当
的通项公式;(Ⅱ)①当 为奇数时,比较
为奇数时,比较 与
与 的大小; ②当
的大小; ②当 为偶数时,若
为偶数时,若 ,问是否存在常数
,问是否存在常数 (与n无关),使得等式
(与n无关),使得等式 恒成立,若存在,求出
恒成立,若存在,求出 的值;若不存在,说明理由
的值;若不存在,说明理由
 的公比为
的公比为 ,首项为
,首项为 ,其前
,其前 项的和为
项的和为 .数列
.数列 的前
的前 项的和为
项的和为 , 数列
, 数列 的前
的前 项的和为
项的和为
(Ⅰ)若
 ,
, ,求
,求 的通项公式;(Ⅱ)①当
的通项公式;(Ⅱ)①当 为奇数时,比较
为奇数时,比较 与
与 的大小; ②当
的大小; ②当 为偶数时,若
为偶数时,若 ,问是否存在常数
,问是否存在常数 (与n无关),使得等式
(与n无关),使得等式 恒成立,若存在,求出
恒成立,若存在,求出 的值;若不存在,说明理由
的值;若不存在,说明理由解:(Ⅰ)∵
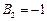 , ∴
, ∴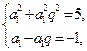 ∴
∴ 或
或 ………………2分
………………2分
∴ ,或
,或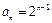 . ……………………………………4分
. ……………………………………4分
(Ⅱ) ∵ 常数,
常数,  =常数,
=常数,
∴数列 ,
,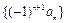 均为等比数列,首项分别为
均为等比数列,首项分别为 ,
, ,公比分别为
,公比分别为 ,
,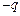 .………………6分
.………………6分
①当 为奇数时, 当
为奇数时, 当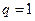 时,
时, 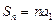 ,
, ,
,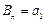 , ∴
, ∴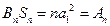 .
.
当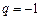 时,
时,  ,
, ,
,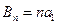 , ∴
, ∴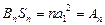 . ……………………8分
. ……………………8分
当 时, 设
时, 设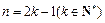 ,
,
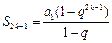 ,
,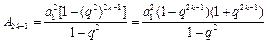 ,
, ,
,
∴ . 综上所述,当
. 综上所述,当 为奇数时,
为奇数时, . ……………………10分
. ……………………10分
②当 为偶数时,∵
为偶数时,∵ ,∴
,∴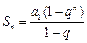 ,
, ,
, .
.
∴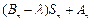 =
=

 =
=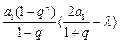 ………………………………12分
………………………………12分
由题设, 对所有的偶数n恒成立,又
对所有的偶数n恒成立,又 ,∴
,∴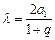 .………………13分
.………………13分
∴存在常数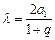 ,使得等式
,使得等式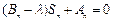 恒成立.………………………………14分
恒成立.………………………………14分

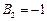 , ∴
, ∴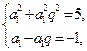 ∴
∴ 或
或 ………………2分
………………2分∴
 ,或
,或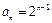 . ……………………………………4分
. ……………………………………4分(Ⅱ) ∵
 常数,
常数,  =常数,
=常数,∴数列
 ,
,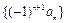 均为等比数列,首项分别为
均为等比数列,首项分别为 ,
, ,公比分别为
,公比分别为 ,
,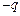 .………………6分
.………………6分 ①当
 为奇数时, 当
为奇数时, 当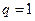 时,
时, 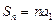 ,
, ,
,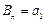 , ∴
, ∴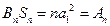 .
. 当
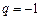 时,
时,  ,
, ,
,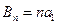 , ∴
, ∴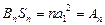 . ……………………8分
. ……………………8分当
 时, 设
时, 设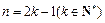 ,
,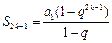 ,
,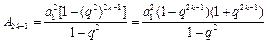 ,
, ,
,∴
 . 综上所述,当
. 综上所述,当 为奇数时,
为奇数时, . ……………………10分
. ……………………10分②当
 为偶数时,∵
为偶数时,∵ ,∴
,∴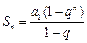 ,
, ,
, .
.∴
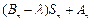 =
=

 =
=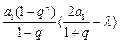 ………………………………12分
………………………………12分由题设,
 对所有的偶数n恒成立,又
对所有的偶数n恒成立,又 ,∴
,∴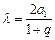 .………………13分
.………………13分∴存在常数
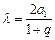 ,使得等式
,使得等式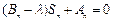 恒成立.………………………………14分
恒成立.………………………………14分略

练习册系列答案
相关题目
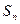 是正项数列
是正项数列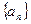 的前n项和且
的前n项和且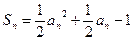 .
.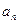 ; (2)
; (2)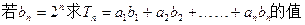
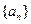 的前12项(如下表所示),按如此规律下去,则
的前12项(如下表所示),按如此规律下去,则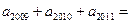
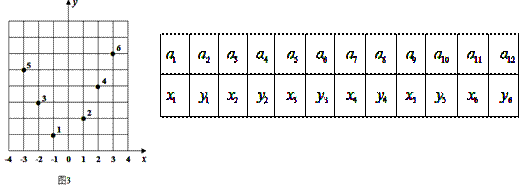
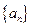 的前
的前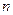 项和为
项和为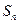 ,已知
,已知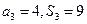 。
。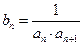 ,求数列
,求数列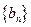 的前10项和.K
的前10项和.K (an+2)2.
(an+2)2. an﹣30,求数列{bn}的前n项和的最小值.
an﹣30,求数列{bn}的前n项和的最小值.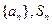 是其前
是其前 项和,且
项和,且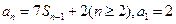 .
.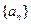 的通项公式;
的通项公式;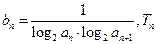 是数列
是数列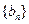 的前
的前 ,求T10的值
,求T10的值 }中,
}中,
 求{
求{
 满足;
满足;
 时,求
时,求 并由此猜测
并由此猜测 的一个通项公式;
的一个通项公式; 时,证明对所有的
时,证明对所有的 ,
,
 。
。 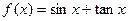 ,项数为27的等差数列
,项数为27的等差数列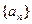 满足
满足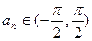 ,且公差
,且公差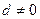 ,若
,若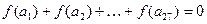 ,则当
,则当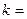 ________________时,
________________时,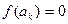 。
。