Question

设A、B是非空集合，则“A⊆B”是“A∪B=B”的（　　）

A．充分不必要条件

B．必要不充分条件

C．充要条件

D．不充分不必要条件

Answer 1

分析：先判断出若“A⊆B”成立，“A∪B=B”一定成立；反之，若“A∪B=B”成立，“A⊆B”成立，利用充要条件的定义得到答案．

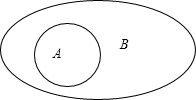
解答：解：若“A⊆B”成立，由韦恩图得到“A∪B=B”一定成立；
反之，若“A∪B=B”成立，由韦恩图得到“A⊆B”成立，

所以“A⊆B”是“A∪B=B”的充要条件，
故选C．

点评：判断一个条件是另一个条件的什么条件，一个两边互相推一下，然后根据充要条件的有关定义加以判断，属于基础题．