题目内容
【题目】已知函数 ![]() 存在两个极值点.
存在两个极值点.
(Ⅰ)求实数a的取值范围;
(Ⅱ)设x1和x2分别是f(x)的两个极值点且x1<x2 , 证明: ![]() .
.
【答案】解:(Ⅰ)由题设函数f(x)的定义域为(0,+∞),f'(x)=lnx﹣ax,
故函数f(x)有两个极值点等价于其导函数f'(x)在(0,+∞)有两个零点.
当a=0时f'(x)=lnx,显然只有1个零点x0=1.
当a≠0时,令h(x)=lnx﹣ax,那么 ![]() .
.
若a<0,则当x>0时h'(x)>0,即h(x)单调递增,所以h(x)无两个零点.
若a>0,则当 ![]() 时h'(x)>0,h(x)单调递增;当
时h'(x)>0,h(x)单调递增;当 ![]() 时h'(x)<0,h(x)单调递减,
时h'(x)<0,h(x)单调递减,
所以 ![]() .
.
又h(1)=﹣a<0,当x→0时→﹣∞,故若有两个零点,则 ![]() ,得
,得 ![]() .
.
综上得,实数a的取值范围是 ![]() .
.
(Ⅱ)证明:要证 ![]() ,两边同时取自然对数得
,两边同时取自然对数得 ![]() .
.
由f'(x)=0得 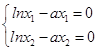 ,得
,得 ![]() .
.
所以原命题等价于证明 ![]() .
.
因为x1<x2,故只需证 ![]() ,即
,即 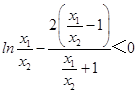 .
.
令 ![]() ,则0<t<1,设
,则0<t<1,设 ![]() ,只需证g(t)<0.
,只需证g(t)<0.
而 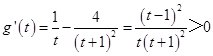 ,故g(t)在(0,1)单调递增,所以g(t)<g(1)=0.
,故g(t)在(0,1)单调递增,所以g(t)<g(1)=0.
综上得 ![]() .
.
【解析】(Ⅰ)函数f(x)有两个极值点等价于其导函数f'(x)在(0,+∞)有两个零点,分类讨论求实数a的取值范围;(Ⅱ)要证 ![]() ,两边同时取自然对数得
,两边同时取自然对数得 ![]() ,由f'(x)=0得
,由f'(x)=0得 ![]() ,得
,得 ![]() .所以原命题等价于证明
.所以原命题等价于证明 ![]() .
.
【考点精析】掌握利用导数研究函数的单调性和函数的极值与导数是解答本题的根本,需要知道一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;求函数
在这个区间单调递减;求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值.
是极小值.

 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案【题目】某公司为了了解一年内的用水情况,抽取了10天的用水量如下表所示:
天数 | 1 | 1 | 1 | 2 | 2 | 1 | 2 |
用水量/吨 | 22 | 38 | 40 | 41 | 44 | 50 | 95 |
(Ⅰ)在这10天中,该公司用水量的平均数是多少?每天用水量的中位数是多少?
(Ⅱ)你认为应该用平均数和中位数中的哪一个数来描述该公司每天的用水量?