题目内容
(本小题满分16分)
已知函数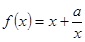 的定义域为(0,
的定义域为(0,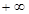 ),且
),且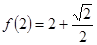 ,设点P是函数图象上的任意一点,过点P分别作直线
,设点P是函数图象上的任意一点,过点P分别作直线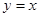 和
和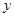 轴的垂线,垂足分别为M、N.
轴的垂线,垂足分别为M、N.
(1)求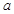 的值;
的值;
(2)问: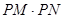 是否为定值?若是,则求出该定值,若不是,请说明理由;
是否为定值?若是,则求出该定值,若不是,请说明理由;
(3)设O为坐标原点,求四边形OMPN面积的最小值.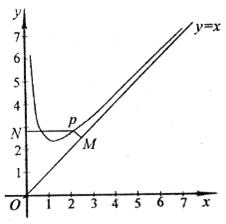
已知函数
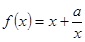 的定义域为(0,
的定义域为(0,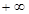 ),且
),且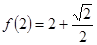 ,设点P是函数图象上的任意一点,过点P分别作直线
,设点P是函数图象上的任意一点,过点P分别作直线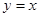 和
和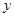 轴的垂线,垂足分别为M、N.
轴的垂线,垂足分别为M、N.(1)求
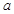 的值;
的值;(2)问:
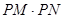 是否为定值?若是,则求出该定值,若不是,请说明理由;
是否为定值?若是,则求出该定值,若不是,请说明理由;(3)设O为坐标原点,求四边形OMPN面积的最小值.

(1)a= ;(2)PM·PN="1." (3)四边形OMPN面积的最小值
;(2)PM·PN="1." (3)四边形OMPN面积的最小值 .
.
 ;(2)PM·PN="1." (3)四边形OMPN面积的最小值
;(2)PM·PN="1." (3)四边形OMPN面积的最小值 .
. (1)由f(2)=2+ 直接建立关于a的方程,解出a值.
直接建立关于a的方程,解出a值.
(II) 设 ,则PM=
,则PM= =
= ,PN=
,PN= ,显然
,显然 .
.
(III)设 ,则直线PM:y-
,则直线PM:y- 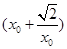 ="-"
="-"  ,
,
再与y=x联立,可解出M(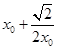 ,
,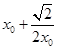 ),根据
),根据 建立关于x0的函数,然后再考虑采用均值不等式求最值.
建立关于x0的函数,然后再考虑采用均值不等式求最值.
(1)∵f(2)=2+ ,∴2+
,∴2+ =2+
=2+ ,
,
∴a= (4分)
(4分)
(2)设 ,则PM=
,则PM= =
= ,PN=
,PN= ,
,
∴PM·PN=1. (8分)
(3)设 ,则直线PM:y-
,则直线PM:y- 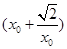 ="-"
="-" 
由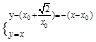 得M(
得M(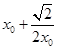 ,
,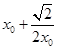 )
)


当且仅当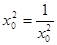 ,即
,即 时取等号,故四边形OMPN面积的最小值
时取等号,故四边形OMPN面积的最小值 .(16分)
.(16分)
 直接建立关于a的方程,解出a值.
直接建立关于a的方程,解出a值.(II) 设
 ,则PM=
,则PM= =
= ,PN=
,PN= ,显然
,显然 .
.(III)设
 ,则直线PM:y-
,则直线PM:y- 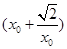 ="-"
="-"  ,
,再与y=x联立,可解出M(
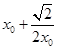 ,
,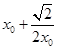 ),根据
),根据 建立关于x0的函数,然后再考虑采用均值不等式求最值.
建立关于x0的函数,然后再考虑采用均值不等式求最值.(1)∵f(2)=2+
 ,∴2+
,∴2+ =2+
=2+ ,
,∴a=
 (4分)
(4分)(2)设
 ,则PM=
,则PM= =
= ,PN=
,PN= ,
,∴PM·PN=1. (8分)
(3)设
 ,则直线PM:y-
,则直线PM:y- 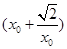 ="-"
="-" 
由
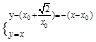 得M(
得M(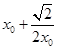 ,
,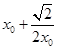 )
)

当且仅当
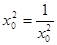 ,即
,即 时取等号,故四边形OMPN面积的最小值
时取等号,故四边形OMPN面积的最小值 .(16分)
.(16分)
练习册系列答案
相关题目
 .
. 是函数
是函数 在区间
在区间 上递增的充分而不必要的条件;
上递增的充分而不必要的条件; 时,满足
时,满足 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.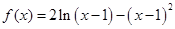 .
.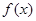 的单调递增区间;
的单调递增区间;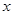 的方程
的方程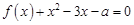 在区间
在区间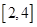 内恰有两个相异的实根,求实数
内恰有两个相异的实根,求实数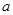 的取值范围.
的取值范围.  为奇函数,
为奇函数,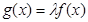
 在
在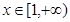 上恒成立,求
上恒成立,求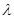 的取值范围。
的取值范围。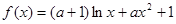 .
.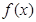 的单调性;
的单调性;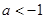 .如果对任意
.如果对任意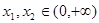 ,
,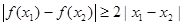 ,求
,求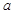 的取值范围.
的取值范围. 的单调递减区间是
的单调递减区间是



 的导函数为
的导函数为 ,
, ,f(x)与x轴恰有一个交点,则
,f(x)与x轴恰有一个交点,则 的最小值为 ( )
的最小值为 ( ) 

 在区间
在区间 上是减函数,则
上是减函数,则 的最小值是( )
的最小值是( )  是减函数的区间为( )
是减函数的区间为( )

