题目内容
13.已知O、A、B、C四点均在半径为$\frac{5\sqrt{2}}{4}$的球S的表面上,并且满足∠BOC=90°,OA⊥平面BOC,AB=AC=$\sqrt{7}$,则三棱锥O-ABC的体积为$\frac{11\sqrt{6}}{24}$.分析 由题意,设OA=x,OB=OC=y,则x2+y2=7,x2+y2+y2=(2×$\frac{5\sqrt{2}}{4}$)2,可得x=$\frac{\sqrt{6}}{2}$,y=$\frac{\sqrt{22}}{2}$,即可求出三棱锥O-ABC的体积.
解答 解:由题意,设OA=x,OB=OC=y,则x2+y2=7,x2+y2+y2=(2×$\frac{5\sqrt{2}}{4}$)2,
∴x=$\frac{\sqrt{6}}{2}$,y=$\frac{\sqrt{22}}{2}$,
∴三棱锥O-ABC的体积为$\frac{1}{3}$•$\frac{1}{2}$•$\frac{\sqrt{22}}{2}$•$\frac{\sqrt{22}}{2}$•$\frac{\sqrt{6}}{2}$=$\frac{11\sqrt{6}}{24}$.
故答案为:$\frac{11\sqrt{6}}{24}$.
点评 本题考查三棱锥O-ABC的体积,考查学生的计算能力,正确求出OA,OB是关键.

练习册系列答案
相关题目
8.已知$\frac{2}{x}$+$\frac{3}{y}$=2(x>0,y>0),则xy的最小值为( )
| A. | 2 | B. | 6 | C. | $\frac{1}{6}$ | D. | $\frac{1}{2}$ |
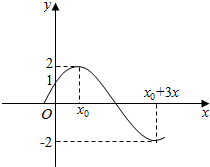 已知函数f(x)=Asin(ωx+φ),(A>0,ω>0,0<φ<π)的图象如图
已知函数f(x)=Asin(ωx+φ),(A>0,ω>0,0<φ<π)的图象如图 