题目内容
20.若a,b∈R+,且a>b,则a+$\frac{1}{(a-b)b}$≥3.分析 先由基本不等式可得(a-b)b≤$\frac{{a}^{2}}{4}$,可得a+$\frac{1}{(a-b)b}$≥a+$\frac{4}{{a}^{2}}$=$\frac{a}{2}$+$\frac{a}{2}$+$\frac{4}{{a}^{2}}$,再由基本不等式可得.
解答 解:∵a,b∈R+,且a>b,∴a-b>0,
∴(a-b)b≤$(\frac{a-b+b}{2})^{2}$=$\frac{{a}^{2}}{4}$,
∴a+$\frac{1}{(a-b)b}$≥a+$\frac{4}{{a}^{2}}$=$\frac{a}{2}$+$\frac{a}{2}$+$\frac{4}{{a}^{2}}$≥3$\root{3}{\frac{a}{2}•\frac{a}{2}•\frac{4}{{a}^{2}}}$=3
当且仅当a-b=b且$\frac{a}{2}$=$\frac{4}{{a}^{2}}$即a=2且b=1时取等号
故答案为:3.
点评 本题考查基本不等式求最值,连续利用基本不等式并注意等号成立的条件是解决问题的关键,属中档题.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案
相关题目
8.已知$\frac{2}{x}$+$\frac{3}{y}$=2(x>0,y>0),则xy的最小值为( )
| A. | 2 | B. | 6 | C. | $\frac{1}{6}$ | D. | $\frac{1}{2}$ |
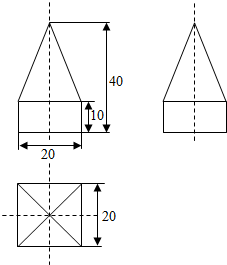 如图所示为一个多面组合体的三视图(单位:cm)
如图所示为一个多面组合体的三视图(单位:cm)