题目内容
14.已知函数f(x)为定义在R上的奇函数,当x>0时,都有f(x+$\frac{3}{2}$)f(x)=2014,且当x∈(0,$\frac{3}{2}$]时,f(x)=log2(2x+1),则f(-2015)+f(2013)=log23.分析 由已知f(x+$\frac{3}{2}$)f(x)=2014,求出函数f(x)的周期,利用已知函数的解析式求解函数值即可.
解答 解:由f(x)为奇函数可得f(-x)=-f(x),再由条件当x>0时,都有f( )f(x)=2014,
可得f(x+$\frac{3}{2}$)=$\frac{2014}{f(x)}$,
所以,f(3+x)=$\frac{2014}{f(x+\frac{3}{2})}$=$\frac{2014}{\frac{2014}{f(x)}}$=f(x).函数的周期是3,
当x∈(0,$\frac{3}{2}$]时,f(x)=log2(2x+1),
所以,f(-2015)+f(2013)
=-f(2015)+f(2013)
=-f(671×3)+f(671×3)
=-f(2)+f(0)
=-f(-1)
=f(1)
=log23.
故答案为:log23.
点评 本题主要考察函数奇偶性的性质,函数的周期,函数值的求法,属于中档题.

练习册系列答案
相关题目
4.已知M={y∈R|y=|x|},N={x∈R|x=y2},则下列关系中正确的是( )
| A. | M?N | B. | M=N | C. | M≠N | D. | N?M |
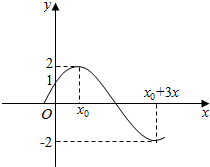 已知函数f(x)=Asin(ωx+φ),(A>0,ω>0,0<φ<π)的图象如图
已知函数f(x)=Asin(ωx+φ),(A>0,ω>0,0<φ<π)的图象如图 