题目内容
10.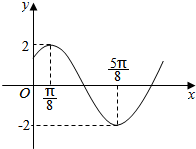 已知函数y=2sin(ωx+$\frac{π}{4}$)在一个周期内的图象如图所示:
已知函数y=2sin(ωx+$\frac{π}{4}$)在一个周期内的图象如图所示:(1)求函数f(x)的最大值和最小正周期;
(2)求函数f(x)的单调递减区间.
分析 (1)由函数的图象可得函数的最大值和最小正周期.
(2)根据函数的解析式以及正弦函数的单调性,求得函数的减区间.
解答 解:(1)根据函数y=2sin(ωx+$\frac{π}{4}$)在一个周期内的图象,可得$\frac{T}{2}$=$\frac{1}{2}$•$\frac{2π}{ω}$=$\frac{5π}{8}$-$\frac{π}{8}$=$\frac{π}{2}$,求得ω=2,T=π,
显然函数的最大值为2.
(2)由(1)可得函数y=2sin(2x+$\frac{π}{4}$),令2kπ+$\frac{π}{2}$≤2x+$\frac{π}{4}$≤2kπ+$\frac{3π}{2}$,求得kπ+$\frac{π}{8}$≤x≤kπ+$\frac{5π}{8}$,
故函数的减区间为[kπ+$\frac{π}{8}$,kπ+$\frac{5π}{8}$],k∈Z.
点评 本题主要考查正弦函数的周期性和单调性,属于基础题.

练习册系列答案
相关题目
20.函数f(x)=$\sqrt{(x+3)^{2}+1}$+$\sqrt{(x-5)^{2}+4}$,则函数f(x)的值域是( )
| A. | [$\sqrt{73}$,+∞) | B. | (+∞,$\sqrt{73}$] | C. | [-$\sqrt{73}$,$\sqrt{73}$] | D. | [-$\sqrt{36}$,$\sqrt{36}$] |