题目内容
设椭圆 的左、右焦点分别为
的左、右焦点分别为 ,
,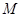 为椭圆上异于长轴端点的一点,
为椭圆上异于长轴端点的一点, ,△
,△ 的内心为I,则
的内心为I,则 ( )
( )
A. | B. | C. | D. |
A
解析试题分析:由题意,|MF1|+|MF2|=4,而|F1F2|=2 ,
,
设圆与MF1、MF2,分别切于点A,B,根据切线长定理就有|F1F2|=|F1A|+|F2B|=2 ,
,
所以|MI|cosθ=|MA|=|MB|= ,故选A.
,故选A.
考点:椭圆的定义,椭圆的几何性质,圆的切线长定理。
点评:小综合题,将椭圆的基础知识与圆的知识综合考查,难度不大,注意结合图形特征,寻求解题途径。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
直线 与曲线
与曲线 的交点个数为( )
的交点个数为( )
| A.4个 | B.1个 | C.2个 | D.3个 |
已知双曲线 的一个焦点与抛物线
的一个焦点与抛物线 的焦点重合,且双曲线的离心率等于
的焦点重合,且双曲线的离心率等于 ,则该双曲线的方程为( )
,则该双曲线的方程为( )
A. | B. | C.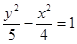 | D. |
已知抛物线Cl:y2= 2x的焦点为F1,抛物线C2:y=2x2的焦点为F2,则过F1且与F1F2垂直的直线 的一般方程式为
的一般方程式为
| A.2x- y-l=0 | B.2x+ y-1=0 |
| C.4x-y-2 =0 | D.4x-3y-2 =0 |
 :
: 的离心率为
的离心率为 ,双曲线
,双曲线 的渐近线与椭圆
的渐近线与椭圆



 为抛物线
为抛物线 上一个动点,直线
上一个动点,直线 :
: ,
, :
: ,则
,则



 的左焦点
的左焦点 ,作圆:
,作圆: 的切线,切点为E,延长FE交双曲线右支于点P,若
的切线,切点为E,延长FE交双曲线右支于点P,若 ,则双曲线的离心率为( )
,则双曲线的离心率为( )



 的双曲线与圆
的双曲线与圆 的一个交点,则
的一个交点,则 = ( )
= ( )



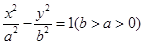 ,过右焦点
,过右焦点 作双曲线的其中一条渐近线的垂线
作双曲线的其中一条渐近线的垂线 ,垂足为
,垂足为 ,交另一条渐近线于
,交另一条渐近线于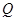 点,若
点,若 (其中
(其中 为坐标原点),则双曲线的离心率为( )
为坐标原点),则双曲线的离心率为( )


