题目内容
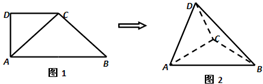 如图1,在直角梯形ABCD中,∠ADC=90°,CD∥AB,AB=4,AD=CD=2.将△ADC沿AC折起,使平面ADC⊥平面ABC,得到几何体D-ABC,如图2所示.
如图1,在直角梯形ABCD中,∠ADC=90°,CD∥AB,AB=4,AD=CD=2.将△ADC沿AC折起,使平面ADC⊥平面ABC,得到几何体D-ABC,如图2所示.(Ⅰ)求证:BC⊥平面ACD;
(Ⅱ)求几何体D-ABC的体积.
分析:(Ⅰ)解法一:由题中数量关系和勾股定理,得出AC⊥BC,再证BC垂直与平面ACD中的一条直线即可,△ADC是等腰Rt△,底边上的中线OD垂直底边,由面面垂直的性质得OD⊥平面ABC,所以OD⊥BC,从而证得BC⊥平面ACD;
解法二:证得AC⊥BC后,由面面垂直,得线面垂直,即证.
(Ⅱ),由高和底面积,求得三棱锥B-ACD的体积即是几何体D-ABC的体积.
解法二:证得AC⊥BC后,由面面垂直,得线面垂直,即证.
(Ⅱ),由高和底面积,求得三棱锥B-ACD的体积即是几何体D-ABC的体积.
解答: 解:(Ⅰ)
解:(Ⅰ)
【解法一】:在图1中,由题意知,AC=BC=2
,∴AC2+BC2=AB2,∴AC⊥BC
取AC中点O,连接DO,则DO⊥AC,又平面ADC⊥平面ABC,
且平面ADC∩平面ABC=AC,DO?平面ACD,从而OD⊥平面ABC,
∴OD⊥BC
又AC⊥BC,AC∩OD=O,
∴BC⊥平面ACD
【解法二】:在图1中,由题意,得AC=BC=2
,∴AC2+BC2=AB2,∴AC⊥BC
∵平面ADC⊥平面ABC,平面ADC∩平面ABC=AC,BC?面ABC,∴BC⊥平面ACD
(Ⅱ)由(Ⅰ)知,BC为三棱锥B-ACD的高,且BC=2
,S△ACD=
×2×2=2,
所以三棱锥B-ACD的体积为:VB-ACD=
Sh=
×2×2
=
,
由等积性知几何体D-ABC的体积为:
.
 解:(Ⅰ)
解:(Ⅰ)【解法一】:在图1中,由题意知,AC=BC=2
| 2 |
取AC中点O,连接DO,则DO⊥AC,又平面ADC⊥平面ABC,
且平面ADC∩平面ABC=AC,DO?平面ACD,从而OD⊥平面ABC,
∴OD⊥BC
又AC⊥BC,AC∩OD=O,
∴BC⊥平面ACD
【解法二】:在图1中,由题意,得AC=BC=2
| 2 |
∵平面ADC⊥平面ABC,平面ADC∩平面ABC=AC,BC?面ABC,∴BC⊥平面ACD
(Ⅱ)由(Ⅰ)知,BC为三棱锥B-ACD的高,且BC=2
| 2 |
| 1 |
| 2 |
所以三棱锥B-ACD的体积为:VB-ACD=
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
4
| ||
| 3 |
由等积性知几何体D-ABC的体积为:
4
| ||
| 3 |
点评:本题通过平面图形折叠后得立体图形,考查空间中的垂直关系,重点是“线线垂直,线面垂直,面面垂直”的转化;等积法求体积,也是常用的数学方法.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目


 (2013•海淀区二模)如图1,在直角梯形ABCD中,∠ABC=∠DAB=90°,∠CAB=30°,BC=2,AD=4.把△DAC沿对角线AC折起到△PAC的位置,如图2所示,使得点P在平面ABC上的正投影H恰好落在线段AC上,连接PB,点E,F分别为线段PA,PB的中点.
(2013•海淀区二模)如图1,在直角梯形ABCD中,∠ABC=∠DAB=90°,∠CAB=30°,BC=2,AD=4.把△DAC沿对角线AC折起到△PAC的位置,如图2所示,使得点P在平面ABC上的正投影H恰好落在线段AC上,连接PB,点E,F分别为线段PA,PB的中点.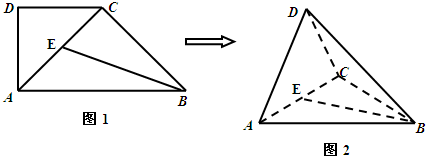 (1)求证:DA⊥BC;
(1)求证:DA⊥BC;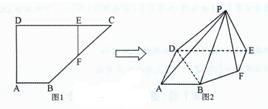 如图1,在直角梯形ABCD中,AB∥CD,∠A=90°,AB=2,CD=6,AD=3,E为CD上一点,且DE=4,过E作EF∥AD交BC于F现将△CEF沿EF折起到△PEF,使∠PED=60°,如图2.
如图1,在直角梯形ABCD中,AB∥CD,∠A=90°,AB=2,CD=6,AD=3,E为CD上一点,且DE=4,过E作EF∥AD交BC于F现将△CEF沿EF折起到△PEF,使∠PED=60°,如图2.