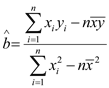题目内容
【题目】如图,在边长为2的正方形![]() 中,
中,![]() 分别为
分别为![]() 的中点,
的中点,![]() 为
为![]() 的中点,沿
的中点,沿![]() 将正方形折起,使
将正方形折起,使![]() 重合于点
重合于点![]() ,在构成的四面体
,在构成的四面体![]() 中,下列结论错误的是
中,下列结论错误的是
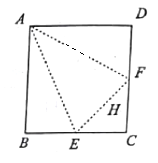
A. ![]() 平面
平面![]()
B. 直线![]() 与平面
与平面![]() 所成角的正切值为
所成角的正切值为![]()
C. 四面体![]() 的内切球表面积为
的内切球表面积为![]()
D. 异面直线![]() 和
和![]() 所成角的余弦值为
所成角的余弦值为![]()
【答案】C
【解析】
由![]() 可判断
可判断![]() ;连接
;连接![]() ,则
,则![]() 为
为![]() 与平面
与平面![]() 所成的角,求出正切值可判断
所成的角,求出正切值可判断![]() ;设四面体
;设四面体![]() 内切球半径为
内切球半径为![]() ,表面积为
,表面积为![]() ,体积为
,体积为![]() ,利用
,利用![]() 求出半径可判断
求出半径可判断![]() ;取
;取![]() 的中点
的中点![]() ,可得
,可得![]() 为异面直线
为异面直线![]() 和
和![]() 所成角,求出余弦值可判断
所成角,求出余弦值可判断![]() .
.

翻折前,![]() ,故翻折后,
,故翻折后,![]() ,
,
又![]() 平面
平面![]() ,故
,故![]() 正确.
正确.
连接![]() ,则
,则![]() 为
为![]() 与平面
与平面![]() 所成的角,
所成的角,
![]() ,
,![]() 是
是![]() 的中点,
的中点,![]() ,
,
![]() ,又
,又![]() ,
,![]() ,故
,故![]() 正确.
正确.
设四面体![]() 内切球半径为
内切球半径为![]() ,表面积为
,表面积为![]() ,体积为
,体积为![]() ,
,
则![]() ,又因为
,又因为![]() ,
,
![]() ,
,
所以![]() ,内切球的表面积为
,内切球的表面积为![]() ,
,![]() 错,
错,
取![]() 的中点
的中点![]() ,连接
,连接![]() ,则
,则![]() ,
,
![]() 为异面直线
为异面直线![]() 和
和![]() 所成角,
所成角,
![]() ,
,
![]() ,
,
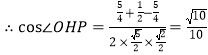 ,故
,故![]() 正确,故选C.
正确,故选C.

练习册系列答案
相关题目