题目内容
(本题满分12分)
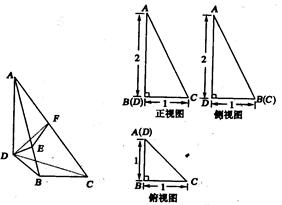
如图所示,已知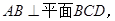 M、N分别是AC、AD的中点,BC
M、N分别是AC、AD的中点,BC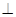 CD.
CD.
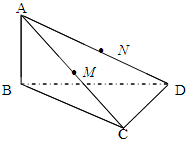
(Ⅰ)求证:MN∥平面BCD;
(Ⅱ)求证:平面B CD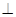 平面ABC;
平面ABC;
(Ⅲ)若AB=1,BC=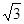 ,求直线AC与平面BCD所成的角.
,求直线AC与平面BCD所成的角.
如图所示,已知
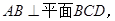 M、N分别是AC、AD的中点,BC
M、N分别是AC、AD的中点,BC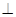 CD.
CD.
(Ⅰ)求证:MN∥平面BCD;
(Ⅱ)求证:平面B CD
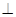 平面ABC;
平面ABC;(Ⅲ)若AB=1,BC=
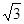 ,求直线AC与平面BCD所成的角.
,求直线AC与平面BCD所成的角.(1)见解析(2)见解析;(3)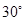 .
.
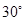 .
.本试题主要是考查了线面平行的证明以及面面垂直的正迷宫和线面角的求解的综合运用。
(1)因为因为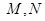 分别是
分别是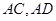 的中点,所以
的中点,所以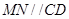 ,利用线面平行的判定定理得到。
,利用线面平行的判定定理得到。
(2)因为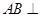 平面
平面 ,
, 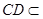 平面
平面 ,所以
,所以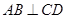 .
.
又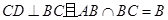 ,所以
,所以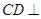 平面
平面 .
.
(3)因为AB=1,BC=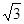 ,求直线AC与平面BCD所成的角,故所以
,求直线AC与平面BCD所成的角,故所以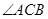 为直线
为直线 与平面
与平面 所成的角.解三角形得到结论。
所成的角.解三角形得到结论。
解 (1)因为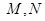 分别是
分别是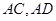 的中点,所以
的中点,所以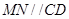 .
.
又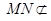 平面
平面 且
且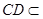 平面
平面 ,所以
,所以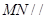 平面
平面 .………………..4分
.………………..4分
(2)因为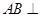 平面
平面 ,
, 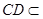 平面
平面 ,所以
,所以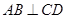 .
.
又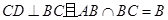 ,所以
,所以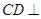 平面
平面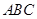 .
.
又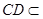 平面
平面 ,所以平面
,所以平面 平面
平面 .。。。。。。。。。。。。。。。。。。。。。。8分
.。。。。。。。。。。。。。。。。。。。。。。8分
(3)因为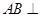 平面
平面 ,所以
,所以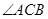 为直线
为直线 与平面
与平面 所成的角.
所成的角.
在直角 中,
中, ,所以
,所以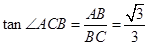 .所以
.所以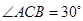 .
.
故直线 与平面
与平面 所成的角为
所成的角为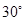 .………………….12分
.………………….12分
(1)因为因为
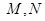 分别是
分别是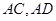 的中点,所以
的中点,所以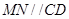 ,利用线面平行的判定定理得到。
,利用线面平行的判定定理得到。(2)因为
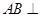 平面
平面 ,
, 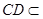 平面
平面 ,所以
,所以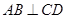 .
.又
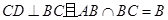 ,所以
,所以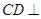 平面
平面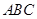 .
.(3)因为AB=1,BC=
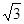 ,求直线AC与平面BCD所成的角,故所以
,求直线AC与平面BCD所成的角,故所以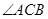 为直线
为直线 与平面
与平面 所成的角.解三角形得到结论。
所成的角.解三角形得到结论。解 (1)因为
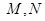 分别是
分别是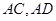 的中点,所以
的中点,所以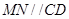 .
.又
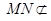 平面
平面 且
且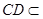 平面
平面 ,所以
,所以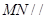 平面
平面 .………………..4分
.………………..4分 (2)因为
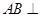 平面
平面 ,
, 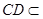 平面
平面 ,所以
,所以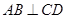 .
.又
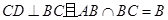 ,所以
,所以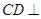 平面
平面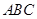 .
.又
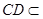 平面
平面 ,所以平面
,所以平面 平面
平面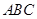 .。。。。。。。。。。。。。。。。。。。。。。8分
.。。。。。。。。。。。。。。。。。。。。。。8分 (3)因为
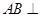 平面
平面 ,所以
,所以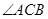 为直线
为直线 与平面
与平面 所成的角.
所成的角. 在直角
 中,
中, ,所以
,所以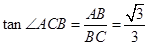 .所以
.所以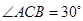 .
.故直线
 与平面
与平面 所成的角为
所成的角为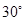 .………………….12分
.………………….12分 
练习册系列答案
相关题目
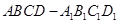 中,
中,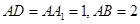 ,点
,点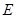 在棱
在棱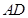 上移动
上移动 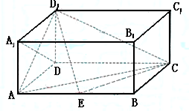
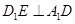 ;
;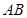 的中点时,求点
的中点时,求点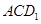 的距离;
的距离;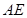 等于何值时,二面角
等于何值时,二面角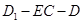 的大小为
的大小为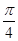
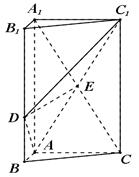
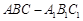 中,
中,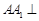 平面
平面 ,
,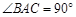 ,
,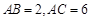 , 点
, 点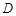 在线段
在线段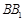 上,且
上,且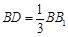 ,
,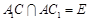 .
.
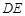 与平面
与平面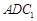 与平面
与平面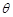 ,若
,若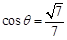 ,求
,求 的长;
的长;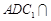 平面
平面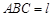 ,求直线
,求直线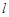 与
与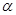 ,则b与
,则b与 平面
平面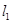 ,
,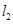 ,
,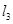 是空间三条不同的直线,则下列命题正确的是( )
是空间三条不同的直线,则下列命题正确的是( )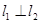 ,
,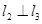
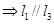
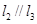
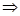
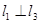
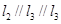
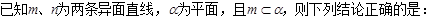 ( )
( )
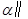 平面
平面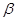 的是( )
的是( )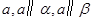
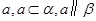
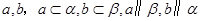
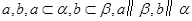
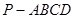 中,
中,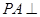 底面
底面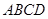 ,
,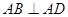 ,
,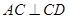 ,
,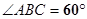 ,
,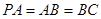 ,
,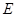 是
是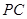 的中点.
的中点.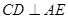 ;
;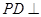 平面
平面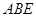 ;
;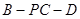 的余弦值.
的余弦值.