题目内容
如图所示,矩形ABCD中,AB=a,AD=b,过点D作DE⊥AC于E,交直线AB于F.现将△ACD沿对角线AC折起到△PAC的位置,使二面角P AC
AC B的大小为60°.过P作PH⊥EF于H.
B的大小为60°.过P作PH⊥EF于H.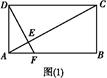
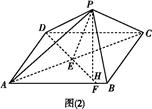
(1)求证:PH⊥平面ABC;
(2)若a+b=2,求四面体P ABC体积的最大值.
ABC体积的最大值.
(1)见解析 (2) 
解析(1)证明:∵DF⊥AC,
∴折起后AC⊥PE,AC⊥EF,
∴AC⊥平面PEF,
又PH?平面PEF,
∴AC⊥PH,
又PH⊥EF,EF∩AC=E,
∴PH⊥平面ABC.
(2)解:∵PE⊥AC,EF⊥AC,
∴∠PEF就是二面角P AC
AC B的平面角,
B的平面角,
∴∠PEF=60°,
∴Rt△PHE中,PH=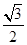 PE,
PE,
折起前,Rt△ADC中,
DE= =
=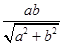 ,
,
S△ABC=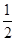 ab,
ab,
折起后,PE=DE,
∴PH=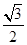 PE=
PE=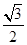 ·
·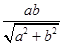 ,
,
∴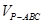 =
=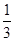 PH·S△ABC
PH·S△ABC
=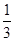 ·
·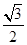 ·
·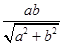 ·
·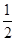 ab
ab
= ·
· ,
,
∵a+b=2,a>0,b>0,
∴ ≤
≤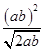 =
=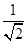
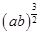 ≤
≤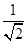
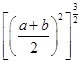 =
=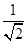 ,
,
当且仅当a=b=1时,两个等号同时成立,
因此(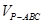 )max=
)max= .
.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
 中,已知
中,已知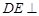 平面
平面 ,
,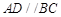 ,
,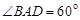 ,
,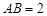 ,
,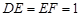 .
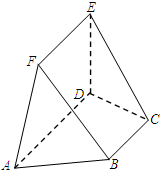
.
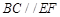 ;
;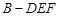 的体积.
的体积.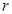 的一个实心球,使球与水面恰好相切,试求取出球后水面高为多少?
的一个实心球,使球与水面恰好相切,试求取出球后水面高为多少?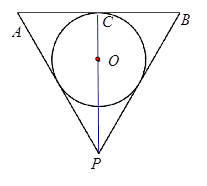
 ,AD=2,求四边形ABCD绕AD旋转一周所成几何体的表面积及体积.
,AD=2,求四边形ABCD绕AD旋转一周所成几何体的表面积及体积.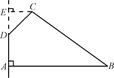
 是边长为
是边长为 的正三角形,
的正三角形, ,
, 平面
平面 ,平面
,平面 平面
平面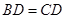 ,且
,且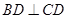 .
.
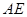 //平面
//平面 ;
; 平面
平面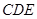 ;
;
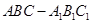 中,侧面
中,侧面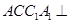 平面
平面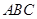 ,
,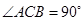 ,
,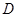 为
为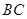 中点.
中点.
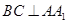 ;
;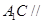 平面
平面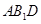 ;
;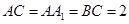 ,
,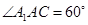 ,求三棱锥
,求三棱锥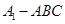 的体积.
的体积.
