题目内容
如图,三角形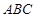 中,
中,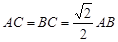 ,
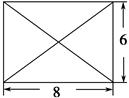
,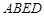 是边长为
是边长为 的正方形,平面
的正方形,平面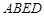 ⊥底面
⊥底面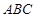 ,若
,若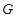 、
、 分别是
分别是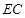 、
、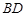 的中点.
的中点.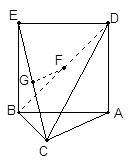
(1)求证: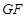 ∥底面
∥底面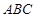 ;
;
(2)求证: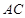 ⊥平面
⊥平面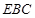 ;
;
(3)求几何体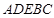 的体积.
的体积.
详见解析
解析试题分析:(1)根据:面面平行,线面平行的定理,所以取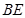 的中点
的中点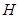 ,连
,连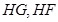 ,
,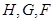 分别为
分别为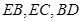 的中点,所以
的中点,所以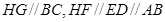 ,然后根据面面平行的判定定理证明面
,然后根据面面平行的判定定理证明面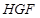 //面
//面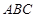 ,进一步证得
,进一步证得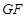 ∥底面
∥底面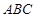 ;(2)根据
;(2)根据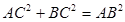 ,证得
,证得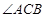 是直角,根据面面垂直,的性质定理,结合
是直角,根据面面垂直,的性质定理,结合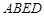 是边长为
是边长为 的正方形,得
的正方形,得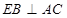 ,证得线线垂直,线面垂直;(3)取
,证得线线垂直,线面垂直;(3)取 中点
中点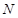 ,即
,即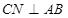 ,几何体
,几何体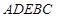 看成四棱锥
看成四棱锥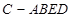 的体积,代入公式
的体积,代入公式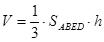 ,根据面面垂直,线面垂直的性质定理等可证,
,根据面面垂直,线面垂直的性质定理等可证,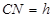 ,代入数字,得到结果.
,代入数字,得到结果.
试题解析:(I)解:取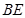 的中点
的中点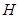 ,连结
,连结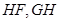 ,(如图)
,(如图)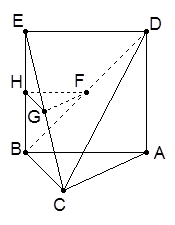
因为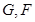 分别是
分别是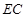 和
和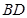 的中点,
的中点,
所以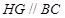 ,
,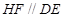 , 2分
, 2分
又因为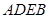 为正方形, 所以
为正方形, 所以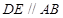 ,从而
,从而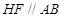 ,
,
所以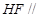 平面
平面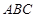 ,
,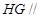 平面
平面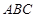 ,
,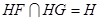 ,
,
所以平面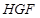 //平面
//平面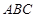 ,
,
所以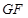 //平面
//平面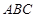 .
.
(2)因为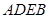 为正方形,所以
为正方形,所以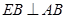 ,所以
,所以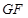
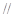 平面
平面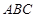 , 4分
, 4分
又因为平面 ⊥平面
⊥平面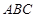 ,所以
,所以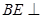 平面
平面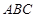 , 6分
, 6分
所以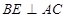 ,
,
又因为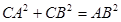 ,
,
所以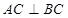 ,
,
因为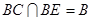 ,
,
所以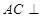 平面
平面 . 8分
. 8分
(3)连结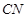 ,因为
,因为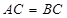 ,所以
,所以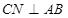 , 9分
, 9分
又平面 ⊥平面
⊥平面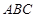 ,
,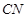 平面
平面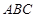 ,所以
,所以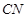 ⊥平面
⊥平面 。
。
因为三角形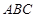 是等腰直角三角形,所以
是等腰直角三角形,所以

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
 是边长为
是边长为 的正三角形,
的正三角形, ,
, 平面
平面 ,平面
,平面 平面
平面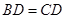 ,且
,且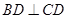 .
.
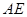 //平面
//平面 ;
; 平面
平面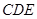 ;
;
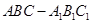 中,侧面
中,侧面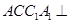 平面
平面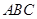 ,
,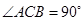 ,
,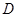 为
为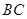 中点.
中点.
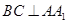 ;
;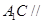 平面
平面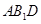 ;
;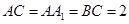 ,
,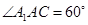 ,求三棱锥
,求三棱锥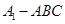 的体积.
的体积.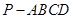 中,底面
中,底面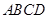 为直角梯形,且
为直角梯形,且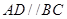 ,
,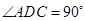 ,平面
,平面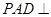 底面
底面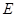 为
为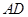 的中点,
的中点,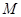 是棱
是棱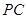 的中点,
的中点, .
.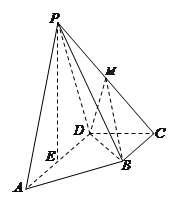

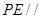 平面
平面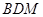 ;
;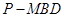 的体积.
的体积. 中,AC⊥BC,AB⊥
中,AC⊥BC,AB⊥ ,
,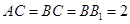 ,D为AB的中点,且CD⊥
,D为AB的中点,且CD⊥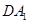 。
。
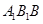 ⊥平面ABC;
⊥平面ABC;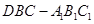 的体积。
的体积。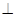 平面ABCD,四边形ABCD为矩形,PA=AB=
平面ABCD,四边形ABCD为矩形,PA=AB= ,AD=1,点F是PB的中点,点E在边BC上移动.
,AD=1,点F是PB的中点,点E在边BC上移动.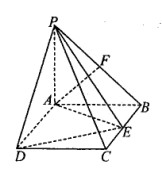
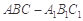 中,侧棱与底面垂直,
中,侧棱与底面垂直,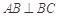 ,
,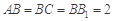 ,
,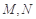 分别是
分别是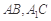 的中点
的中点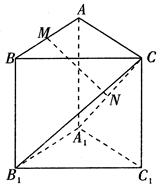
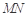 ∥平面
∥平面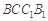 ;
; ;
; 的体积.
的体积.