题目内容
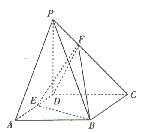
【题目】如图,三棱柱![]() 中,侧面
中,侧面![]() 是边长为2的菱形,且
是边长为2的菱形,且![]() ,
, ![]() ,四棱锥
,四棱锥![]() 的体积为2,点
的体积为2,点![]() 在平面
在平面![]() 内的正投影为
内的正投影为![]() ,且
,且![]() 在
在![]() 上,点
上,点![]() 在线段
在线段![]() 上,且
上,且![]() .
.
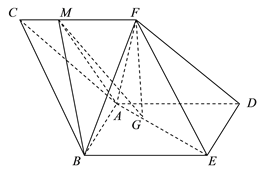
(Ⅰ)证明:直线![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值.
的余弦值.
【答案】(Ⅰ)证明见解析;(Ⅱ) ![]() .
.
【解析】试题分析:(1)通过构造辅助线FH,证明![]() 为平行四边形,即借助线线平行证明线面平行;(2)借助底面四边形的对角线互相垂直,建立空间直角坐标,利用向量方法求解二面角.
为平行四边形,即借助线线平行证明线面平行;(2)借助底面四边形的对角线互相垂直,建立空间直角坐标,利用向量方法求解二面角.
(Ⅰ)解析:
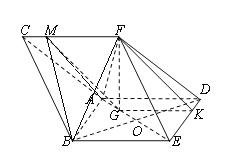
因为四棱锥![]() 的体积为2,
的体积为2,
即![]() ,所以
,所以![]()
又![]() ,所以
,所以![]() 即点
即点![]() 是靠近点
是靠近点![]() 的四等分点,
的四等分点,
过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,所以
,所以![]() ,
,
又![]() ,所以
,所以![]() 且
且![]() ,
,
所以四边形![]() 为平行四边形,
为平行四边形,
所以![]() ,所以直线
,所以直线![]() 平面
平面![]() .
.
(Ⅱ)
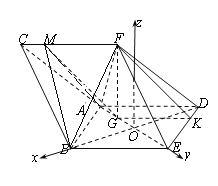
设![]() 的交点为
的交点为![]() ,
, ![]() 所在直线为
所在直线为![]() 轴,
轴, ![]() 所在直线为
所在直线为![]() 轴,过点
轴,过点![]() 作平面
作平面![]() 的垂线为
的垂线为![]() 轴,建立空间直角坐标系,如图所示:
轴,建立空间直角坐标系,如图所示:
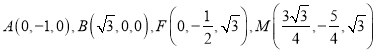
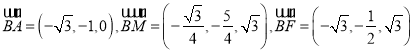
设平面![]() 的法向量为
的法向量为![]() ,
,
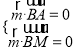 ,则
,则![]() ,
, 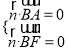 ,则
,则![]()
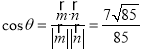 ,即为所求.
,即为所求.

练习册系列答案
相关题目
【题目】某花店每天以每枝5元的价格从农场购进若干枝玫瑰花,然后以每枝10元的价格出售.如果当天卖不完,剩下的玫瑰花作垃圾处理.
(1)若花店一天购进17枝玫瑰花,求当天的利润y(单位:元)关于当天需求量n(单位:枝,n∈N)的函数解析式;
(2)花店记录了100天玫瑰花的日需求量(单位:枝),整理得下表:
日需求量n | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
频数 | 10 | 20 | 16 | 16 | 15 | 13 | 10 |
①假设花店在这100天内每天购进17枝玫瑰花,求这100天的日利润(单位:元)的平均数;
②若花店一天购进17枝玫瑰花,以100天记录的各需求量的频率作为各需求量发生的概率,求当天的利润不少于75元的概率.