题目内容
5.曲线C是平面内与两个定点F1(-1,0)和F2(1,0)的距离的积等于常数a(a>1)的点的轨迹,给出下列四个结论:①曲线C关于坐标轴对称;
②曲线C过点$(0,\sqrt{a-1})$;
③若点P在曲线C上(不在x轴上),则△PF1F2的面积不大于$\frac{1}{2}a$.
其中,所有正确结论的序号是①②③.
分析 设动点坐标为(x,y),由动点与两个定点F1(-1,0)和F2(1,0)的距离的积等于常数a(a>1)可得动点的轨迹方程,然后由方程特点判断①;把点的坐标代入方程判断②;设出曲线上动点,结合①得到动点纵坐标,代入三角形面积公式利用配方法求出最大值判断③.
解答 解:对于①,由题意设动点坐标为(x,y),则利用题意及两点间的距离公式的得:[(x+1)2+y2]•[(x-1)2+y2]=a2,
取x=-x,或y=-y,所得方程不变,曲线C关于坐标轴对称,①正确;
对于②,把点$(0,\sqrt{a-1})$代入[(x+1)2+y2]•[(x-1)2+y2]=a2,即(1+a-1)(1+a-1)=a2成立,∴曲线C过点$(0,\sqrt{a-1})$,②正确;
对于③,由题意知点P在曲线C上,则△F1PF2的面积${S}_{△{F}_{1}P{F}_{2}}$=$\frac{1}{2}$×2×y=y,由①知y2=-x2-1+$\sqrt{4{x}^{2}+{a}^{2}}$或y2=-x2-1-$\sqrt{4{x}^{2}+{a}^{2}}$(舍去),
令$\sqrt{4{x}^{2}+{a}^{2}}=t$,则x2=$\frac{{t}^{2}-{a}^{2}}{4}$,∴y2=-$\frac{{t}^{2}-{a}^{2}}{4}$-1+t=-$\frac{1}{4}$(t-2)2+$\frac{{a}^{2}}{4}$≤$\frac{{a}^{2}}{4}$,
∴$({S}_{△{F}_{1}P{F}_{2}})^{2}≤\frac{1}{2}a$,故③正确.
故答案为:①②③.
点评 本题考查动点的轨迹方程的求法,训练了曲线的对称性的判断方法,利用解析式选择换元法求函数值域是解答③的关键,是中档题.

| A. | a>b>c | B. | a>c>b | C. | c>b>a | D. | b>c>a |
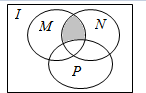 设I是全集,集合M,N,P都是其子集,则图中的阴影部分表示的集合为( )
设I是全集,集合M,N,P都是其子集,则图中的阴影部分表示的集合为( )| A. | M∩(P∩∁IN) | B. | M∩(N∩∁IP) | C. | M∩(∁IN∩∁IM) | D. | (M∩N)∪(M∩P) |
 如图,在长方体ABCD-A1B1C1D1中,直线AB与直线A1C1的位置关系是异面.
如图,在长方体ABCD-A1B1C1D1中,直线AB与直线A1C1的位置关系是异面.