题目内容
16. 如图,在长方体ABCD-A1B1C1D1中,直线AB与直线A1C1的位置关系是异面.
如图,在长方体ABCD-A1B1C1D1中,直线AB与直线A1C1的位置关系是异面.
分析 根据异面直线的定义结合长方体的性质,可得AB与A1C1的位置关系是异面.
解答 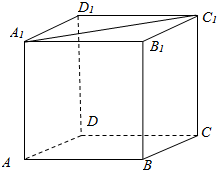 解:∵长方体ABCD-A1B1C1D1中,AB∥A1B1
解:∵长方体ABCD-A1B1C1D1中,AB∥A1B1
∴AB∥平面A1B1C1D1,
而A1C1与A1B1是相交直线,
∴AB与A1C1的位置关系是异面.
故答案为:异面.
点评 本题考查异面直线的判定,是基础题.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
1.两圆(x-1)2+(y+2)2=1与(x+3)2+(y-1)2=16的位置关系是( )
| A. | 内切 | B. | 外切 | C. | 相离 | D. | 相交 |
8.已知函数f(x)=x2+ax-c,g(x)=($\frac{1}{2}$)x-m,若不等式f(x)<0的解集为{x|-2<x<1},若对任意的x1∈[-3,-2],存在x2∈[0,2],使f(x1)≥g(x2),则实数m的取值范围是( )
| A. | m≥$\frac{1}{4}$ | B. | m≥1 | C. | m≥0 | D. | m≥2 |
6.函数f(x)=sin(2x+$\frac{5π}{2}$)是( )
| A. | 奇函数 | B. | 偶函数 | ||
| C. | 既不是奇函数又是偶函数 | D. | 既不是奇函数也不是偶函数 |
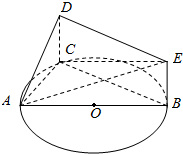 如图,AB是圆O的直径,C是圆O上异于A、B的一个动点,DC垂直于圆O所在的平面,DC∥EB,DC=EB=1,AB=4.
如图,AB是圆O的直径,C是圆O上异于A、B的一个动点,DC垂直于圆O所在的平面,DC∥EB,DC=EB=1,AB=4.