题目内容
(本题满分14分)设函数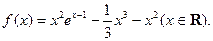 (1)求函数
(1)求函数 的单调区间;(2)求
的单调区间;(2)求 在[—1,2]上的最小值;(3)当
在[—1,2]上的最小值;(3)当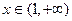 时,用数学归纳法证明:
时,用数学归纳法证明: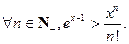
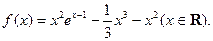 (1)求函数
(1)求函数 的单调区间;(2)求
的单调区间;(2)求 在[—1,2]上的最小值;(3)当
在[—1,2]上的最小值;(3)当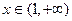 时,用数学归纳法证明:
时,用数学归纳法证明: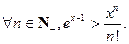
(Ⅰ)增区间为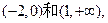
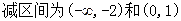 … (Ⅱ) 见解析
… (Ⅱ) 见解析
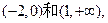
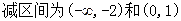 … (Ⅱ) 见解析
… (Ⅱ) 见解析(1)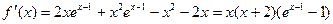 …………2分
…………2分
令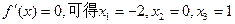
函数 的增区间为
的增区间为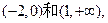
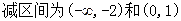 …………5分
…………5分
(2)当

所以 ………………8分
………………8分
(3)设
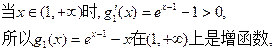
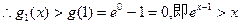 ; ………………10分
; ………………10分
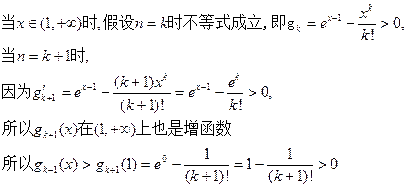
即当 时,不等式成立。
时,不等式成立。
所以当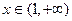 时,
时, ………………14分
………………14分
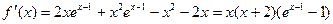 …………2分
…………2分令
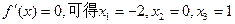
 | 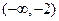 | —2 | (-2,0) | 0 | (0,1) | 1 |  |
 | — | 0 | + | 0 | — | 0 | + |
 | 减 | 极小 | 增 | 极大 | 减 | 极小 | 增 |
 的增区间为
的增区间为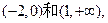
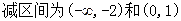 …………5分
…………5分(2)当


所以
 ………………8分
………………8分(3)设

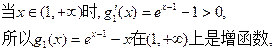
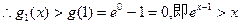 ; ………………10分
; ………………10分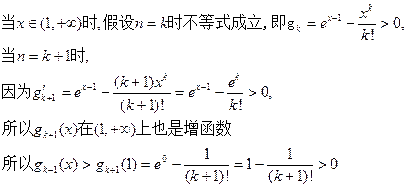
即当
 时,不等式成立。
时,不等式成立。所以当
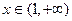 时,
时, ………………14分
………………14分
练习册系列答案
相关题目
 是函数
是函数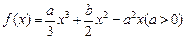 的两个极值点,且
的两个极值点,且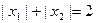
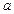 的取值范围;
的取值范围;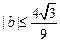 .
.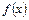 的导函数
的导函数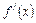 满足
满足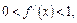 常数
常数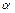 为方程
为方程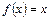
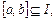 存在
存在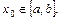 使等式
使等式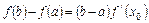 成立。 求证:方程
成立。 求证:方程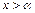 时,总有
时,总有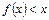 成立。
成立。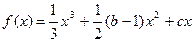 (b、c为常数).
(b、c为常数).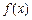 在
在
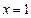 和
和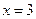 处取得极值,试求
处取得极值,试求 的值;
的值;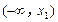 、
、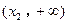 上单调递增,且在
上单调递增,且在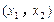 上单调递减,又满足
上单调递减,又满足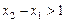 ,求证:
,求证: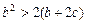 。
。 (1)求函数
(1)求函数 ;?(2)若存在常数k和b,使得函数
;?(2)若存在常数k和b,使得函数 对其定义域内的任意实数
对其定义域内的任意实数 分别满足
分别满足 则称直线
则称直线 的“隔离直线”.试问:函数
的“隔离直线”.试问:函数 是否存在“隔离直线”?若存在,求出“隔离直线”方程,不存在,请说明理由.
是否存在“隔离直线”?若存在,求出“隔离直线”方程,不存在,请说明理由.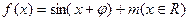 为奇函数,且过点
为奇函数,且过点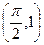 ,函数
,函数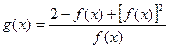 .
.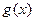 的解析式并求其定义域;
的解析式并求其定义域;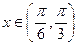 时不等式
时不等式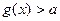 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.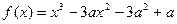
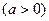
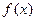 的单调区间;
的单调区间;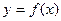 在点
在点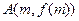 和
和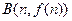
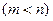 处的切线都与
处的切线都与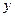 轴垂直,若曲线
轴垂直,若曲线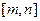 上与
上与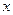 轴相交,求实数
轴相交,求实数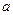 的取值范围;
的取值范围;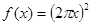 的导数是( )
的导数是( )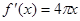
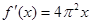
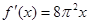
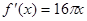
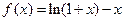 ,
,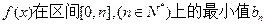 ;
;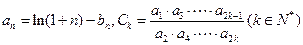 ,
,