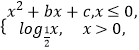题目内容
【题目】关于x的方程 
（a＞0，且a≠1）解的个数是（ ）
A.2
B.1
C.0
D.不确定的
【答案】A
【解析】解：由题意ax=﹣x2+2x+a，﹣x2+2x+a＞0．
令f（x）=ax，g（x）=﹣x2+2x+a，（1）当a＞1时，
f（x）=ax在（﹣∞，+∞）上单调递增，且f（0）=1，f（1）=a，
g（x）=﹣x2+2x+a在[0，1]上单调递增，在[1，+∞）上单调递减，且g（0）=a，g（1）=1+a，
在[0，1]上，f（x）＜g（x），
∵g（x）在x＜0及x＞1时分别有一个零点，而f（x）恒大于零，
∴f（x）与g（x）的图象在x＜0及x＞1时分别有一个交点，
∴方程有两个解；（2）当a＜1时，
f（x）=ax在（﹣∞，+∞）上单调递减，且f（0）=1，f（1）=a，
g（x）=﹣x2+2x+a在[0，1]上单调递增，在[1，+∞）上单调递减，且g（0）=a，g（1）=1+a，
f（0）＞g（0），f（1）＜g（1），
∴在（0，1）上f（x）与g（x）有一个交点，
又g（x）在x＞1时有一个零点，而f（x）恒大于零，
∴f（x）与g（x）的图象在x＞1时还有一个交点，
∴方程有两个解．
综上所述，方程有两个解．
所以答案是：A．
练习册系列答案
智慧小复习系列答案
相关题目
