题目内容
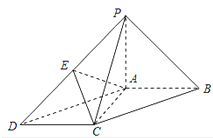
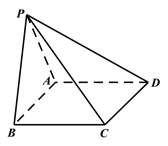
【题目】如图,四棱锥![]() 的底面
的底面![]() 为平行四边形,平面
为平行四边形,平面![]() 平面
平面![]() ,
, ![]() ,
,![]() .
.
(Ⅰ)求证: ![]() ;
;
(Ⅱ)若三角形![]() 是边长为
是边长为![]() 的等边三角形,求三棱锥
的等边三角形,求三棱锥![]() 外接球的表面积.
外接球的表面积.
【答案】(Ⅰ)见解析;(Ⅱ)![]() .
.
【解析】试题分析:(Ⅰ)本问证明线线垂直,可以先证线面垂直,再证线线垂直,即证明AB垂直于PC所在平面,过P作![]() 于
于![]() ,根据面面垂直性质定理可知,PO
,根据面面垂直性质定理可知,PO![]() 面
面![]() ,易知PO
,易知PO![]() AB,再证明OC
AB,再证明OC![]() AB即可;(Ⅱ)求三棱锥
AB即可;(Ⅱ)求三棱锥![]() 的外接球,关键是找到外接球的球心,因为三角形
的外接球,关键是找到外接球的球心,因为三角形![]() 是边长为
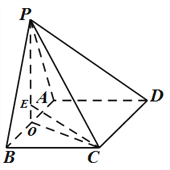
是边长为![]() 的等边三角形,设E为三角形
的等边三角形,设E为三角形![]() 的重心,显然EP=EA=EB,再通过证明EC=EB,于是可以得出EA=EB=EC=EP,则可以说明E为外接球的球心,于是可以求外接球半径,再求三棱锥
的重心,显然EP=EA=EB,再通过证明EC=EB,于是可以得出EA=EB=EC=EP,则可以说明E为外接球的球心,于是可以求外接球半径,再求三棱锥![]() 外接球的表面积.
外接球的表面积.
试题解析: (Ⅰ)作![]() 于
于![]() ……①,连接
……①,连接![]() ,
,
∵平面![]() 平面
平面![]() ,且
,且![]() ,
,
∴![]() 面
面![]() .
.
∵![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
又∵![]() ,∴
,∴![]() ……②
……②
又![]() ,由①②,得
,由①②,得![]() 面
面![]() ,
,
又![]() 面
面![]() ,∴
,∴![]() .
.
(Ⅱ)∵三角形![]() 是边长为
是边长为![]() 的等边三角形,∴
的等边三角形,∴![]() .
.
∵![]() 面
面![]() ,
, ![]() ,线段
,线段![]() 上取点
上取点![]() ,∴
,∴![]() ,
,
![]() 是外接球的球心,设三棱锥
是外接球的球心,设三棱锥![]() 外接球的半径为
外接球的半径为![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
∴![]() .
.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目