题目内容
8.已知数列{an}中,a1,a2,…,ak是以4为首项、-2为公差的等差数列,ak+1,ak+2,…,a2k是以$\frac{1}{2}$为首项、$\frac{1}{2}$为公比的等比数列(k≥3,k∈N*),且对任意的n∈N*,都有an+2k=an成立,Sn是数列{an}的前n项和.(1)当k=5时,求a48的值;
(2)判断是否存在k,使S4k+3≥18.
分析 (1)根据等差数列的通项公式得出ak,等比数列的通项公式得出ak+n,再由an+2k=an,得数列{an}为周期是2k的数列,由此求出a48;
(2)根据数列{an}的周期性,化简并判断使a4k+3≥18是否成立.
解答 解:(1)根据等差数列的通项公式,得
ak=4+(k-1)•(-2)=-2k+6;
根据等比数列的通项公式,得
ak+k=$\frac{1}{2}$•${(\frac{1}{2})}^{k-1}$=${(\frac{1}{2})}^{k}$;
又∵对一切正整数n,都有an+2k=an成立,
∴数列{an}为周期数列,且周期为2k;
当k=5时,周期为10,
∴a48=a8=a5+3,
∴a48是等比数列中的第三项,
∴a48=${(\frac{1}{2})}^{3}$=$\frac{1}{8}$;
(2)假设存在k,使a4k+3≥18成立,
∵数列{an}为周期数列,且周期为2k,
∴a4k+3=a3=0≥18不成立,
即不存在k使a4k+3≥18.
点评 本题考查了等差与等比数列的应用问题,也考查了归纳方法的应用问题,是综合性题目.

练习册系列答案
相关题目
20.为了了解两种手机电池的待机时间,研究人员分别对甲、乙两种电池做了7次测试,测试结果统计如下表所示:
(Ⅰ)试计算7次测试中,甲、乙两种电池的待机时间的平均值和方差,并判断哪种电池的性能比较好,简单说明理由.
(Ⅱ)为了深入研究乙电池的性能,研究人员从乙电池待机时间测试的7组数据中随机抽取2组分析,求2组数据均大于121的概率.
| 测试次数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 甲电池待机时间(h) | 120 | 125 | 122 | 124 | 124 | 123 | 123 |
| 乙电池待机时间(h) | 118 | 123 | 127 | 120 | 124 | 120 | 122 |
(Ⅱ)为了深入研究乙电池的性能,研究人员从乙电池待机时间测试的7组数据中随机抽取2组分析,求2组数据均大于121的概率.

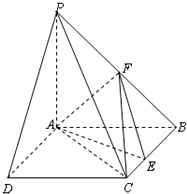 如图所示,PA⊥平面ABCD,ABCD是矩形,AB=1,AD=$\sqrt{3}$,点F是PB的中点,点E在边BC上移动.
如图所示,PA⊥平面ABCD,ABCD是矩形,AB=1,AD=$\sqrt{3}$,点F是PB的中点,点E在边BC上移动. 如图,侧棱垂直底面的三棱柱ABC-A1B1C1的底面ABC位于平行四边形ACDE中,AE=2,AC=AA1=4,∠E=60°,点B,F分别为DE,BC中点.
如图,侧棱垂直底面的三棱柱ABC-A1B1C1的底面ABC位于平行四边形ACDE中,AE=2,AC=AA1=4,∠E=60°,点B,F分别为DE,BC中点.