题目内容
11.根据十八大的精神,全国在逐步推进教育教学制度改革,各高校自主招生在高考录取中所占的比例正在逐渐加大.对此,某高校在今年的自主招生考试中制定了如下的规则:笔试阶段,考生从6道备选试题中一次性抽取3道题,并独立完成所抽取的3道题,至少正确完成其中2道试题则可以进入面试.已知考生甲正确完成每道题的概率为$\frac{2}{3}$,且每道题正确完成与否互不影响;考生乙能正确完成6道试题中的4道题,另外2道题不能完成.(Ⅰ)求考生甲至少正确完成2道题的概率;(Ⅱ)求考生乙能通过笔试进入面试的概率;
(Ⅲ)记所抽取的三道题中考生乙能正确完成的题数为ξ,求ξ的分布列和数学期望.
分析 (Ⅰ)利用独立重复试验的概率公式,求考生甲至少正确完成2道题的概率;
(Ⅱ)确定基本事件数,即可求出考生乙能通过笔试进入面试的概率;
(Ⅲ)确定ξ的可能取值,求出相应的概率,即可求ξ的分布列和数学期望.
解答 解:(Ⅰ)设考生甲至少正确完成2道题的概率为P,则P=${C}_{3}^{2}(\frac{2}{3})^{2}•\frac{1}{3}+{C}_{3}^{3}(\frac{2}{3})^{3}$=$\frac{20}{27}$;
(Ⅱ)基本事件总数为${C}_{6}^{3}$=20,考生乙能通过笔试进入面试的基本事件数为${C}_{4}^{3}+{C}_{4}^{2}{C}_{2}^{1}$=16,
所以考生甲至少正确完成2道题的概率为$\frac{16}{20}$=$\frac{4}{5}$;
(Ⅲ)ξ的所有可能取值为1,2,3,则
P(ξ=1)=$\frac{{C}_{4}^{1}{C}_{2}^{2}}{{C}_{6}^{3}}$=$\frac{1}{5}$,P(ξ=2)=$\frac{{C}_{4}^{2}{C}_{2}^{1}}{{C}_{6}^{3}}$=$\frac{3}{5}$,P(ξ=3)=$\frac{{C}_{4}^{3}}{{C}_{6}^{3}}$=$\frac{1}{5}$,
ξ的分布列为:
| ξ | 1 | 2 | 3 |
| P | $\frac{1}{5}$ | $\frac{3}{5}$ | $\frac{1}{5}$ |
点评 本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题,是历年高考的必考题型.

练习册系列答案
相关题目
20.为了了解两种手机电池的待机时间,研究人员分别对甲、乙两种电池做了7次测试,测试结果统计如下表所示:
(Ⅰ)试计算7次测试中,甲、乙两种电池的待机时间的平均值和方差,并判断哪种电池的性能比较好,简单说明理由.
(Ⅱ)为了深入研究乙电池的性能,研究人员从乙电池待机时间测试的7组数据中随机抽取2组分析,求2组数据均大于121的概率.
| 测试次数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 甲电池待机时间(h) | 120 | 125 | 122 | 124 | 124 | 123 | 123 |
| 乙电池待机时间(h) | 118 | 123 | 127 | 120 | 124 | 120 | 122 |
(Ⅱ)为了深入研究乙电池的性能,研究人员从乙电池待机时间测试的7组数据中随机抽取2组分析,求2组数据均大于121的概率.
 设F为抛物线C:x2=2py(p>0)的焦点,点F到直线l:x+y+2=0的距离为$\frac{3}{2}\sqrt{2}$.
设F为抛物线C:x2=2py(p>0)的焦点,点F到直线l:x+y+2=0的距离为$\frac{3}{2}\sqrt{2}$. 将一个半径适当的小球放入如图所示的容器自上方的入口处,小球自由下落,小气在下落的过程中,将遇到黑色障碍物3次,最后落入A袋或B袋中,已知小球每次遇到障碍物时,向左、右两边下落的概率分别是$\frac{1}{3}$,$\frac{2}{3}$
将一个半径适当的小球放入如图所示的容器自上方的入口处,小球自由下落,小气在下落的过程中,将遇到黑色障碍物3次,最后落入A袋或B袋中,已知小球每次遇到障碍物时,向左、右两边下落的概率分别是$\frac{1}{3}$,$\frac{2}{3}$
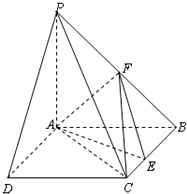 如图所示,PA⊥平面ABCD,ABCD是矩形,AB=1,AD=$\sqrt{3}$,点F是PB的中点,点E在边BC上移动.
如图所示,PA⊥平面ABCD,ABCD是矩形,AB=1,AD=$\sqrt{3}$,点F是PB的中点,点E在边BC上移动. 如图,正方形ADMN与矩形ABCD所在平面互相垂直,AB=2AD=6.
如图,正方形ADMN与矩形ABCD所在平面互相垂直,AB=2AD=6.