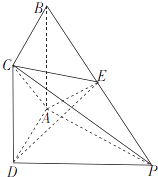
题目内容
【题目】如图，在四棱锥
中，
底面
，底面为矩形，
为
的中点，且
，
，
.
（1）求证：
平面
；
（2）若点
为线段上一点，且
，求四棱锥
的体积.
【答案】（1）见解析 （2）6
【解析】
（1）连接
交
于点
，得出点为的中点，利用中位线的性质得出
，再利用直线与平面平行的判定定理可得出
平面
；
（2）过
作
交
于
，由
平面
，得出
平面，可而出
，结合
，可证明出
平面
，可得出
，并计算出
，利用平行线的性质求出
的长，再利用锥体的体积公式可计算出四棱锥
的体积.
（1）连接交于
，连接
.
四边形为矩形，∴为中点.
又
为
中点，∴
.
又
平面，
平面，
∴平面；
（2）过作交于.
∵平面，∴平面.
又
平面，∴
.
∵，
，
，
平面，
∴平面.连接
，则，
又是矩形，易证
，而
，
，得
，
由得
，∴
.
又矩形的面积为8，∴
.
练习册系列答案
相关题目
【题目】2018年春季，世界各地相继出现流感疫情，这已经成为全球性的公共卫生问题.为了考察某种流感疫苗的效果，某实验室随机抽取100只健康小鼠进行试验，得到如下列联表：
感染 | 未感染 | 总计 | |
注射 | 10 | 40 | 50 |
未注射 | 20 | 30 | 50 |
总计 | 30 | 70 | 100 |
参照附表，在犯错误的概率最多不超过__________的前提下，可认为“注射疫苗”与“感染流感”有关系．
（参考公式：
.）
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】已知关于
与
有表格中的数据，且与线性相关，由最小二乘法得
.
| 2 | 4 | 5 | 6 | 8 |
| 30 | 40 | 60 | 50 | 70 |
（1）求与的线性回归方程；
（2）现有第二个线性模型：
，且
.若与（1）的线性模型比较，哪一个线性模型拟合效果比较好，请说明理由
