题目内容
【题目】如图,四棱锥P﹣ABCD的底面ABCD是正方形,PD⊥平面ABCD,E为PB上的点,且2BE=EP. 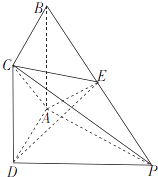
(1)证明:AC⊥DE;
(2)若PC= ![]() BC,求二面角E﹣AC﹣P的余弦值.
BC,求二面角E﹣AC﹣P的余弦值.
【答案】
(1)解:∵PD⊥平面ABCD,AC平面ABCD
∴PD⊥AC
∵底面ABCD是正方形,
∴BD⊥AC,
∵PD、BD是平面PBD内的相交直线,
∴AC⊥平面PBD
∵DE平面PBD,
∴AC⊥DE
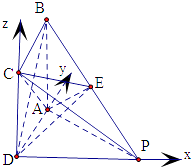
(2)解:分别以DP、DA、DC所在直线为x、y、z轴,建立空间直角坐标系,如图所示
设BC=3,则CP=3 ![]() ,DP=3,结合2BE=EP可得
,DP=3,结合2BE=EP可得
D(0,0,0),A(0,3,0),C(0,0,3),P(3,0,0),
E(1,2,2)
∴ ![]() =(0,3,﹣3),
=(0,3,﹣3), ![]() =(3,0,﹣3),
=(3,0,﹣3), ![]() =(1,2,﹣1)
=(1,2,﹣1)
设平面ACP的一个法向量为 ![]() =(x,y,z),可得
=(x,y,z),可得
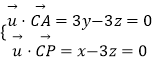 ,取x=1得
,取x=1得 ![]() =(1,1,1)
=(1,1,1)
同理求得平面ACE的一个法向量为 ![]() =(﹣1,1,1)
=(﹣1,1,1)
∵cos< ![]() ,
, ![]() >=
>= ![]() =
= ![]() ,∴二面角E﹣AC﹣P的余弦值等于
,∴二面角E﹣AC﹣P的余弦值等于 ![]()
【解析】(1)由线面垂直的定义,得到PD⊥AC,在正方形ABCD中,证出BD⊥AC,根据线面垂直判定定理证出AC⊥平面PBD,从而得到AC⊥DE;(2)建立空间直角坐标系,如图所示.得D、A、C、P、E的坐标,从而得到 ![]() 、
、 ![]() 、
、 ![]() 的坐标,利用垂直向量数量积为零的方法,建立方程组解出
的坐标,利用垂直向量数量积为零的方法,建立方程组解出 ![]() =(1,1,1)是平面ACP的一个法向量,
=(1,1,1)是平面ACP的一个法向量, ![]() =(﹣1,1,1)是平面ACE的一个法向量,利用空间向量的夹角公式即可算出二面角E﹣AC﹣P的余弦值.
=(﹣1,1,1)是平面ACE的一个法向量,利用空间向量的夹角公式即可算出二面角E﹣AC﹣P的余弦值.

 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案【题目】手机支付也称为移动支付![]() ,是指允许移动用户使用其移动终端(通常是手机)对所消费的商品或服务进行账务支付的一种服务方式.继卡类支付、网络支付后,手机支付俨然成为新宠.某金融机构为了了解移动支付在大众中的熟知度,对15-65岁的人群随机抽样调查,调查的问题是“你会使用移动支付吗?”其中,回答“会”的共有100个人,把这100个人按照年龄分成5组,然后绘制成如图所示的频率分布表和频率分布直方图.
,是指允许移动用户使用其移动终端(通常是手机)对所消费的商品或服务进行账务支付的一种服务方式.继卡类支付、网络支付后,手机支付俨然成为新宠.某金融机构为了了解移动支付在大众中的熟知度,对15-65岁的人群随机抽样调查,调查的问题是“你会使用移动支付吗?”其中,回答“会”的共有100个人,把这100个人按照年龄分成5组,然后绘制成如图所示的频率分布表和频率分布直方图.
组数 | 第l组 | 第2组 | 第3组 | 第4组 | 第5组 |
分组 |
|
|
|
|
|
频数 | 20 | 36 | 30 | 10 | 4 |

(1)求![]() ;
;
(2)从第l,3,4组中用分层抽样的方法抽取6人,求第l,3,4组抽取的人数:
(3)在(2)抽取的6人中再随机抽取2人,求所抽取的2人来自同一个组的概率.
【题目】某中学从高三男生中随机抽取n名学生的身高,将数据整理,得到的频率分布表如表所示:
组号 | 分组 | 频数 | 频率 |
第1组 |
| 5 | 0.05 |
第2组 |
| a | 0.35 |
第3组 |
| 30 | b |
第4组 |
| 20 | 0.20 |
第5组 |
| 10 | 0.10 |
合计 | n | 1.00 | |
(1)求出频率分布表中![]() 的值,并完成下列频率分布直方图;
的值,并完成下列频率分布直方图;
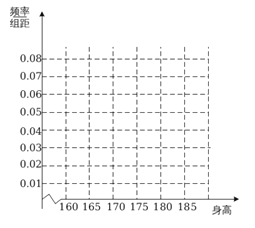
(2)为了能对学生的体能做进一步了解,该校决定在第1,4,5组中用分层抽样取7名学生进行不同项目的体能测试,若在这7名学生中随机抽取2名学生进行引体向上测试,求第4组中至少有一名学生被抽中的概率.
