Question

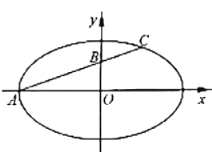
【题目】如图，在平面直角坐标系中，已知椭圆的左顶点为，过的直线交椭圆于另一点，直线交轴于点，且.

（1）求椭圆的离心率；

（2）若椭圆的焦距为，为椭圆上一点，线段的垂直平分线在轴上的截距为（不与轴重合），求直线的方程.

Answer 1

【答案】（1）（2）或

【解析】

(1)设,利用,解得,将其代入椭圆方程可得,再用离心率公式可得;

(2)由(1)及可求得椭圆方程,设的中点为,可求得直线的方程,用中点公式求得点的坐标,将其代入椭圆方程可得一个关于的方程,在直线的方程中令,,也可得一个关于的方程,两个方程联立可解得和,从而可得直线的方程.

（1），设，

因为，

所以，，解得：，，所以，，

因为点在椭圆上，所以有：，即，

所以离心率.

（2）依题意有：，所以，，

又，且，解得：，，

所以椭圆方程为：，

设的中点为，则，故有，

从而的方程为：

令得到，

整理得①,

利用中点公式可得,将其代入椭圆方程得 ,

整理得②,

联立①②方程解得或，

当时,可得直线与轴重合,不合题意舍去,

所以,此时,解得或，

故的方程为或者.