题目内容
【题目】如图所示,在直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=CC1,M,N分别是A1B,B1C1的中点.
(1)求证:MN⊥平面A1BC;
(2)求直线BC1和平面A1BC所成的角的大小.

【答案】(1)见解析;(2)![]()
【解析】试题分析:(1)易得BC⊥平面ACC1A1,连接AC1,则BC⊥AC1.侧面ACC1A1是正方形,所以A1C⊥AC1.又BC∩A1C=C,根据线面垂直的判定定理可知AC1⊥平面A1BC,因为侧面ABB1A1是正方形,MN是△AB1C1的中位线,所以MN∥AC1,从而MN⊥平面A1BC;
(2)根据AC1⊥平面A1BC,设AC1与A1C相交于点D,连接BD,根据线面所成角的定义可知∠C1BD为直线BC1和平面A1BC所成角,设AC=BC=CC1=a,求出C1D,BC1,在Rt△BDC1中,求出∠C1BD,即可求出所求.
试题解析:
(1)证明 如图,由已知BC⊥AC,BC⊥CC1,得BC⊥平面ACC1A1.连接AC1,则BC⊥AC1.
又侧面ACC1A1是正方形,所以A1C⊥AC1.
又BC∩A1C=C,所以AC1⊥平面A1BC.
因为侧面ABB1A1是正方形,M是A1B的中点,连接AB1,则点M是AB1的中点.
又点N是B1C1的中点,则MN是△AB1C1的中位线,所以MN∥AC1.故MN⊥平面A1BC.
(2)如图所示,因为AC1⊥平面A1BC,设AC1与A1C相交于点D,
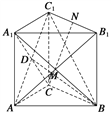
连接BD,则∠C1BD为直线BC1和平面A1BC所成的角.
设AC=BC=CC1=a,则C1D=![]() a,BC1=
a,BC1=![]() a.
a.
在Rt△BDC1中,sin ∠C1BD=![]() =
=![]() ,所以∠C1BD=30°,故直线BC1和平面A1BC所成的角为30°.
,所以∠C1BD=30°,故直线BC1和平面A1BC所成的角为30°.

练习册系列答案
相关题目