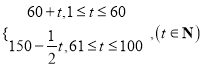Question

【题目】已知f（x）= ，若不等式 对任意的 恒成立，则整数λ的最小值为 ．

Answer 1

【答案】1
【解析】解：∵f（x）= ，

令f（x）＞﹣ ，

解得：x＞ ，

若对任意θ∈[0， ]，不等式f（cos2θ+λsinθ﹣ ）+ ≥0恒成立，

则对任意θ∈[0， ]，cos2θ+λsinθ﹣ ≥ 恒成立，

即1﹣sin2θ+λsinθ﹣ ≥ 恒成立，

当θ=0时，不等式恒成立，

当θ≠0时，1﹣sin2θ+λsinθ﹣ ≥ 可化为：λ≥ =sinθ﹣ ，

当θ= 时，sinθ﹣ 取最大值 ，

故λ＞ ，

故整数λ的最小值为1，

故答案为：1．

令f（x）＞﹣ ，解得：x＞ ，若对任意θ∈[0， ]，不等式f（cos2θ+λsinθ﹣ ）+ ≥0恒成立，则对任意θ∈[0， ]，cos2θ+λsinθ﹣ ≥ 恒成立，进而得到答案．