题目内容
1．方程$\left\{\begin{array}{l}x=t\\ y={t^2}+1\end{array}\right.（{t为参数}）$表示的曲线是（ ）| A． | 直线 | B． | 圆 | C． | 椭圆 | D． | 抛物线 |
分析 由方程$\left\{\begin{array}{l}x=t\\ y={t^2}+1\end{array}\right.（{t为参数}）$，消去t，可得结论．
解答 解：由方程$\left\{\begin{array}{l}x=t\\ y={t^2}+1\end{array}\right.（{t为参数}）$，消去t，可得y=x2+1，
∴表示的曲线是抛物线，
故选：D．
点评 本题考查抛物线的参数方程，考查学生的计算能力，比较基础．
练习册系列答案
相关题目
12．已知x＞0，y＞0，且$\frac{2}{x}$+$\frac{1}{y}$=1，若x+2y＞m2+2m恒成立，则实数m的取值范围是（ ）
| A． | （-4，2） | B． | （-2，0） | C． | （-4，0） | D． | （0，2） |
9．函数f（x）=ex-ex在[0，2]上的最大值为（ ）
| A． | 0 | B． | 1 | C． | e-2 | D． | e（e-2） |
16．为了测得河对岸塔AB的高度，先在河岸上选一点C，使C在塔底B的正东方向上，此时测得塔顶A的仰角为60°．再由点C沿北偏东15°方向走了20米到达点D，测得∠BDC=45°，则塔AB的高度为（ ）
| A． | 20$\sqrt{6}$米 | B． | 20$\sqrt{3}$米 | C． | 20$\sqrt{2}$米 | D． | 20米 |
13．
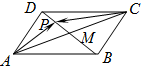如图，平行四边形ABCD的两条对角线相交于点M，点P是MD中点，若|$\overrightarrow{AB}$|=2，|$\overrightarrow{AD}$|=1，且∠BAD=60°，则$\overrightarrow{AP}$$•\overrightarrow{CP}$的值为（ ）
如图，平行四边形ABCD的两条对角线相交于点M，点P是MD中点，若|$\overrightarrow{AB}$|=2，|$\overrightarrow{AD}$|=1，且∠BAD=60°，则$\overrightarrow{AP}$$•\overrightarrow{CP}$的值为（ ）| A． | -$\frac{5}{16}$ | B． | -$\frac{15}{16}$ | C． | -$\frac{25}{16}$ | D． | -$\frac{27}{16}$ |