题目内容
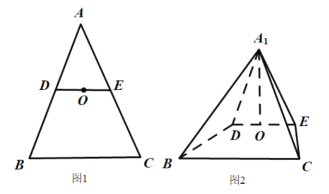
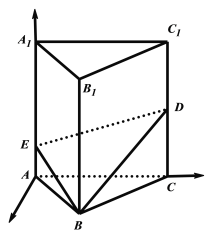
【题目】如图,在棱长都相等的正三棱柱![]() 中,
中,![]() 是棱
是棱![]() 的中点,
的中点,![]() 是棱
是棱![]() 上的动点.设
上的动点.设![]() ,随着
,随着![]() 增大,平面
增大,平面![]() 与底面
与底面![]() 所成锐二面角的平面角是( )
所成锐二面角的平面角是( )

A.增大B.先增大再减小
C.减小D.先减小再增大
【答案】D
【解析】
设正三棱柱![]() 棱长为
棱长为![]() ,设平面
,设平面![]() 与底面
与底面![]() 所成锐二面角为
所成锐二面角为![]() ,
,![]() ,以
,以![]() 为坐标原点建立空间直角坐标系,确定出
为坐标原点建立空间直角坐标系,确定出![]() 点的坐标,求出平面
点的坐标,求出平面![]() 的法向量
的法向量![]() ,底面
,底面![]() 的法向量坐标为
的法向量坐标为![]() ,将
,将![]() 表示为关于
表示为关于![]() 的函数,通过讨论
的函数,通过讨论![]() 的增减变化,即可求出结论.
的增减变化,即可求出结论.
设正三棱柱![]() 棱长为
棱长为![]() ,
,![]() ,
,
设平面![]() 与底面
与底面![]() 所成锐二面角为
所成锐二面角为![]() ,
,
以![]() 为坐标原点,过点
为坐标原点,过点![]() 在底面
在底面![]() 内与
内与![]() 垂直的直线为
垂直的直线为![]() 轴,
轴,
![]() 所在的直线分别为
所在的直线分别为![]() 轴建立空间直角坐标系,
轴建立空间直角坐标系,
则![]() ,
,
设平面![]() 的法向量
的法向量![]() ,则
,则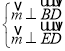 ,
,
即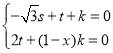 ,令
,令![]() ,则
,则![]() ,
,
所以平面![]() 的一个法向量
的一个法向量![]() ,
,
底面![]() 的一个法向量为
的一个法向量为![]() ,
,
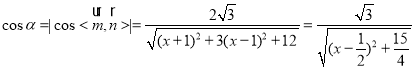
当![]() ,
,![]() 随着
随着![]() 增大而增大,则
增大而增大,则![]() 随着
随着![]() 的增大而减小,
的增大而减小,
当![]() ,
,![]() 随着
随着![]() 增大而减小,则
增大而减小,则![]() 随着
随着![]() 的增大而增大.
的增大而增大.
故选:D.

练习册系列答案
相关题目