题目内容
设二次函数f（x）=x2-x+a（a＞0），若f（m）＜0，则f（m-1）的值为（ ）A．正数
B．负数
C．非负数
D．正数、负数和零都有可能
【答案】分析：先由函数f（x）=x2-x+a（a＞0）的对称轴为x=
，a＞0，以及f（0）=a＞0得到对应的大致图象，再利用f（m）＜0⇒0＜m＜1⇒m-1＜0结合图象即可求得结论．
解答：解：因为函数f（x）=x2-x+a（a＞0）的对称轴为x=
，
又因为a＞0，故f（0）=a＞0对应的大致图象如图：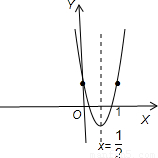
由f（m）＜0⇒0＜m＜1⇒m-1＜0⇒f（m-1）＞0．
故选A．
点评：本题主要考查二次函数的性质，解决本题的关键在于通过已知条件画出对应图象，由图象求出m的取值范围，进而求的结论．
，a＞0，以及f（0）=a＞0得到对应的大致图象，再利用f（m）＜0⇒0＜m＜1⇒m-1＜0结合图象即可求得结论．解答：解：因为函数f（x）=x2-x+a（a＞0）的对称轴为x=
，又因为a＞0，故f（0）=a＞0对应的大致图象如图：
由f（m）＜0⇒0＜m＜1⇒m-1＜0⇒f（m-1）＞0．
故选A．
点评：本题主要考查二次函数的性质，解决本题的关键在于通过已知条件画出对应图象，由图象求出m的取值范围，进而求的结论．
练习册系列答案
相关题目
设二次函数f（x）=ax2+bx+c（a＞0），方程f（x）-x=0的两个根x1、x2满足0＜x1＜x2＜
，且函数f（x）的图象关于直线x=x0对称，则有（ ）
| 1 |
| a |
A、x0≤
| ||
B、x0＞
| ||
C、x0＜
| ||
D、x0≥
|